Chapter 3 Podstawy fizyczne
Teoria dyfrakcji promieni X dzieli się na dwie główne gałęzie: teorię dynamiczną i kinematyczną (inaczej: geometryczną). Pierwsza z nich uwzględnia interferencję fali padającej i fal wielokrotnie ugiętych w krysztale, druga zakłada, że fala padająca ulega w krysztale pojedynczemu ugięciu. Ponadto, teoria kinematyczna zaniedbuje absorpcję i ekstynkcję promieni X w obrębie kryształu, to znaczy zakłada, że na każdy z atomów kryształu pada fala o tej samej amplitudzie. Dlatego teoria kinematyczna stosuje się tylko do kryształów wystarczająco małych, aby spełniały warunek małej absorpcji: , gdzie jest liniowym współczynnikiem absorpcji, zaś - rozmiarem kryształu. W praktyce oznacza to kryształy mniejsze od oraz kryształy mozaikowe [58][28][10]. Nanokryształy spełniają wymogi teorii kinematycznej.
Teoria dyfrakcji ma na celu wyznaczenie natężenia ugiętego promieniowania w funkcji kąta rozproszenia i w zależności od mikroskopowych parametrów charakteryzujących kryształ. Kinematyczna teoria dyfrakcji korzysta z następującego wyrażenia [58]:
| (3.1) |
gdzie jest natężeniem wiązki padającej, jest czynnikiem struktury. Iloczyn jest po trzech wymiarach przestrzeni: są krawędziami komórki elementarnej (jednostkami osiowymi), - liczbami komórek elementarnych w krysztale w każdym z trzech kierunków , zaś jest wektorem rozpraszania. Na podstawie wzoru (3.1) trudno jest wyprowadzić ogólne wyrażenie na profil linii dyfrakcyjnej, jednak spostrzeżenie, że oscylująca funkcja ma to samo maksimum i normalizację co krzywa Gauss’a , skłania do wniosku, że linie bragowskie mają kształt gausowski. Ponieważ mierzone w praktyce linie dyfrakcyjne rzadko bywają podobne do krzywych Gauss’a, przybliża się je często innymi funkcjami, np. Lorentz’a, Voigt’a czy Pearson’a. Ma to zazwyczaj na celu jak najdokładniejsze wyznaczenie średniej ważonej profilu, czyli pozycji refleksu oraz jego natężenia.
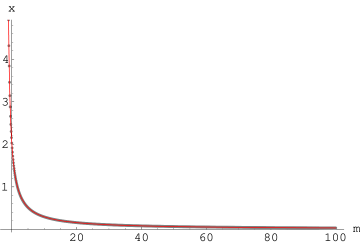
Arbitralność wyboru krzywej opisującej profil linii dyfrakcyjnej jest zrozumiała tak długo, jak długo ten profil jest kształtowany bardziej przez aparaturę pomiarową niż badane kryształy. Szerokość refleksów bragowskich pochodzących od polikryształów mikronowych jest mniejsza niż rozdzielczość dyfraktometrów. Przyjmując, że poszerzenie aparaturowe wysokorozdzielczego dyfraktometru proszkowego wynosi kilka sekund kątowych11 1 Rozdzielczość laboratoryjnych dyfraktometrów proszkowych wynosi typowo kilka minut kątowych. Rozdzielczości sekundowe można uzyskać na dyfraktometrach wysokorozdzielczych (wymaga to użycia monochromatorów krystalicznych)., staje się ono głównym czynnikiem kształtującym profil refleksu dla kryształów większych niż zaś zaburza ten profil już od (rys. 3.1).
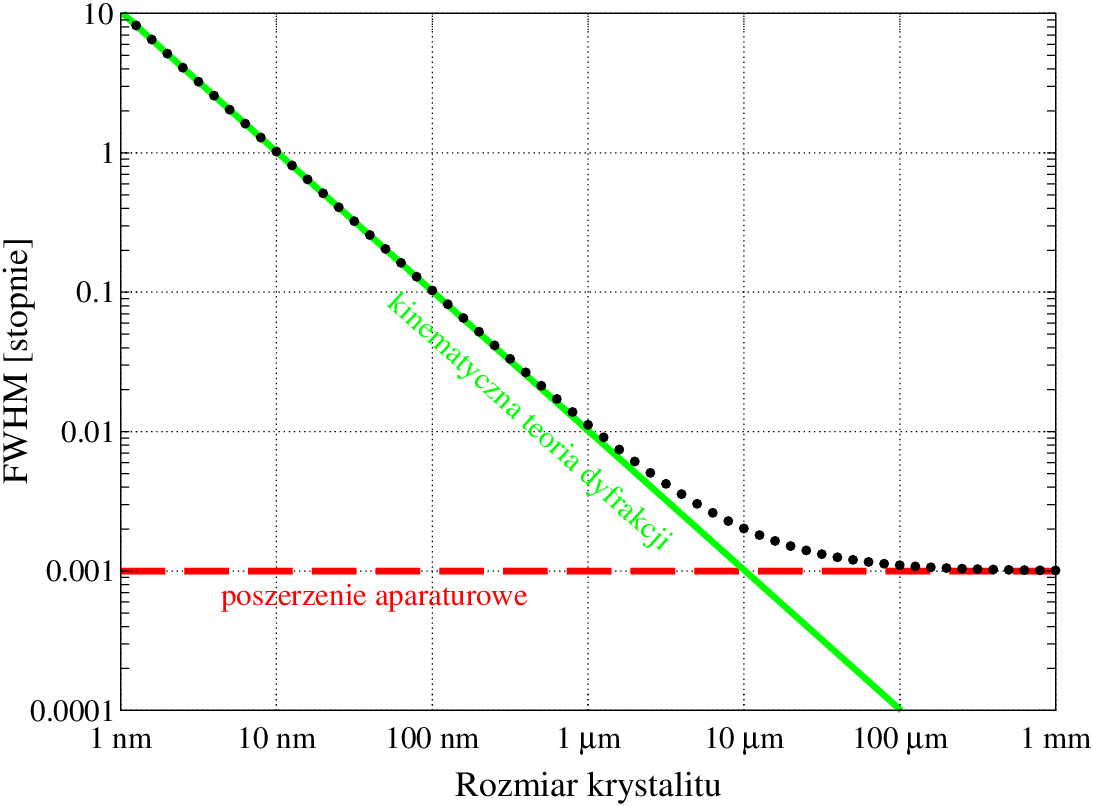
Z drugiej strony, z rys. 3.1 widać, że linie dyfrakcyjne kryształów submikronowych, a szczególnie nanokryształów, są bardzo szerokie i przez to wpływ zniekształceń aparaturowych jest zaniedbywalny. Na profil linii dyfrakcyjnej tak małych krystalitów wpływ ma przede wszystkim mikrostruktura materiału, czyli kształt, rozmiar i naprężenia ziaren. Dokładnych kształtów linii dyfrakcyjnych teoria kinematyczna jednak nie podaje, zaś linie nanoproszków mierzone doświadczalnie nie spełniają gausowskiego przybliżenia kształtu maksimum dyfrakcyjnego.
Punktem wyjścia dalszych rozważań będzie wzór Debye’a, który uzależnia natężenie promieniowania rozproszonego na klasterze atomów uśrednione po wszystkich przestrzennych orientacjach tego klastera, w funkcji wektora rozpraszania . Wzór Debye’a można traktować jako odpowiednik wyrażenia (3.1) dla proszków polikrystalicznych mierzonych w geometrii Debye’a-Scherrer’a. Formuła Debye’a jest stosowana od lat pięćdziesiątych XX wieku do obliczania ab initio dyfraktogramów proszkowych małych układów atomów, zarówno uporządkowanych (kryształy) jak i nieuporządkowanych (ciała amorficzne). W tym rozdziale teoria Debye’a będzie rozwinięta doprowadzając do analitycznych wzorów na profile proszkowych linii dyfrakcyjnych. W rozdziale 4 omówiono zaś metody obliczeń dyfrakcyjnych ab initio.
Dla porządku zaczniemy jednak od wyprowadzenia wzoru Debye’a.
3.1 Interferencja fal
Weźmy pojedynczy elektron, atom lub inny (w dobrym przybliżeniu) punktowy obiekt, na który pada monochromatyczna i równoległa wiązka promieni rentgenowskich. Przyjmijmy, że amplituda padającej fali jest:
| (3.2) |
gdzie jest częstością kątową (lub pulsacją, czyli liczbą pełnych cykli cosinusiody na sekundę), a to czas. Po rozproszeniu na punktowym obiekcie może zmienić się moduł i faza fali rozproszonej. Nową amplitudę można zapisać jako:
| (3.3) |
gdzie wielkość to czynnik rozpraszania, najczęściej atomowy czynnik rozpraszania, czyli siła rozpraszająca obiektu. W przypadku atomów, zależy od liczby elektronów w atomie, czyli od liczby atomowej . Dla promieni rentgenowskich zależy od kąta rozpraszania, dla dyfrakcji neutronów - nie zależy. W każdym razie, jest stały dla danego typu atomów (pierwiastka) i jego wartość odszukuje się z tablic.
Wielkość jest zmianą fazy w czasie rozproszenia. W przypadku rozpraszania na pojedynczym elektronie i (przeważnie) na atomie, . Oznacza to, że promień rozproszony ma fazę przeciwną do padającego. Jeśli zmiana fazy jest identyczna dla wszystkich rozpraszających obiektów, to fakt ten nie wnosi istotnej informacji, dlatego zazwyczaj można go zignorować.
W przypadku rozpraszania jednej fali padającej na grupie wielu obiektów, np. na atomach kryształu, najwygodniej będzie wyrazić jako funkcję wzajemnych położeń tych obiektów względem siebie i względem fali padającej.
3.1.1 Wektor rozpraszania
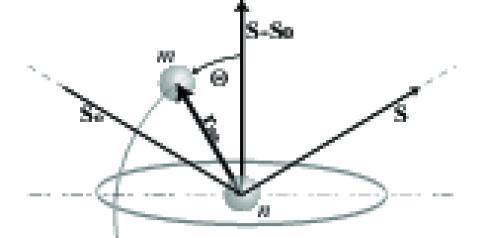
Rozważmy falę padającą jednocześnie na dwa atomy oraz , które umieścimy na końcach wektora , rys. 3.2. Kierunki fali padającej i rozproszonej wyrazimy jako jednostkowe wektory, odpowiednio: i . Kąt pomiędzy wektorami fali padającej i rozproszonej nazwiemy22 2 Potrzeba używania połówki i całości tego kąta zachodzi prawie tak samo często. Nazwanie większego podwojonym skraca zapis bardziej niż nazywanie mniejszego połówkowym. Pozbywamy się wyrażeń typu . . Różnica dróg optycznych fal rozproszonych przez atomy i będzie:
gdzie iloczyny skalarne oraz są, oczywiście, rzutami (cieniami) jednego wektora na drugi. Stąd różnica faz:
| (3.4) |
gdzie to długość fali (zarówno padającej jak i rozproszonej), zaś oznaczony symbolem wektor powstały z różnicy jednostkowych wektorów fali rozproszonej i padającej nazwiemy wektorem rozpraszania:
| (3.5) |
Wektor tworzy podstawę trójkąta równoramiennego zbudowanego z wektorów jednostkowych oraz , pomiędzy którymi kąt wynosi . W takim razie33 3 Wektory jednostkowe i tworzą ramiona trójkąta równoramiennego, którego podstawą jest wektor . Połowa tej podstawy to . Zatem cała podstawa to . długość wektora wynosi . Wynika stąd, że długość (moduł) wektora rozpraszania to:
| (3.6) |
3.1.2 Natężenie fali rozproszonej na grupie atomów
Amplituda fali jest chwilową wartością zmiennego pola elektrycznego w funcji czasu :
| (3.7) |
Jako taka, jest co chwilę inna; jej wartości ciągle się zmieniają od do . Zmieniają się o wiele zbyt szybko (jakieś razy na sekundę), żeby nadążyć z ich rejestracją jakimkolwiek znanym przyrządem. Nie mogąc zmierzyć dostatecznie szybko chwilowej wartości pola elektrycznego, nie znamy także jego aktualnej fazy. To wielka szkoda, ponieważ znając amplitudę i fazę można byłoby rozwiązać prosty układ równań, znaleźć dokładne pozycje rozpraszających obiektów i zbudować tą drogą mikroskop rentgenowski zdolny bezpośrednio pokazać atomy.
Tymczasem, musimy radzić sobie obserwując pod odpowiednio dużymi (mierzalnymi) kątami średnie energie fali rozproszonej. W praktyce mierzymy intensywność plamek na różnego typu detektorach. Plamki te biorą się z reakcji chemicznej (folie fotograficzne), ze wzbudzenia atomów na wyższy poziom energii (image plate), z jonizacji gazu (komory jonizacyjne), itp. W każdym przypadku metodą działania detektora jest konwersja energii kwantu rentgenowskiego do innej, obserwowalnej postaci. Energia fali elektromagnetycznej wyrażana jest tzw. wektorem Poynting’a (gdzie i są, odpowiednio, wektorami pola elektrycznego i magnetycznego fali), a uśredniona energia (moc chwilowa) pola jest , czyli jest uśrednionym kwadratem sinusoidy zmiennego pola elektycznego, zatem - jego amplitudy. Wynika stąd, że do obserwacji wystarczy kwadrat amplitudy, zwany natężeniem fali:
| (3.8) |
Ważną i konieczną własnością natężenia jest nieobecność członu związanego z aktualną fazą fali elektromagnetycznej. Przejście od niemierzalnych amplitud do mierzalnych natężeń polega nie tyle na policzeniu kwadratu lub pierwiastka (co jest łatwe) ile na pozbyciu się czasu z wyrażeń opisujących falę rozproszoną (3.7). Technicznie rzecz biorąc, dla uzyskania natężenia trzeba w wyrażeniu na amplitudę (i) wykreślić człon , (ii) podnieść moduł amplitudy do kwadratu.
Weźmy grupę atomów44 4 Dla uproszczenia zapisu nie podajemy dokładnej liczby atomów, ale pamiętamy, że każde rozproszenie jest równie prawdopodobne i każdy atom “dostaje” ten sam ułamek fali padającej. Odpowiednio, wkłady od rozproszeń na każdym z atomów dają razem 100% fali rozproszonej. W praktyce, normowanie wyniku do liczby rozproszeń nie ma znaczenia, ponieważ obserwowane natężenia są i tak względne (nie znamy liczby oświetlonych atomów). oświetlonych wiązką równoległą o amplitudzie (3.2), podobnie jak na rys. 3.2. Wektory określają położenia atomów względem siebie nawzajem (np. atomu względem atomu ), a nie położenia względem początku układu współrzędnych. Amplituda emitowana w kierunku wektora będzie sumą amplitud wszystkich rozproszeń (3.3). Uwzględniając wyrażenie na różnicę faz (3.4) wyniesie to:
gdzie jest amplitudą fali padającej, jest amplitudą fali rozproszonej, obie sumy przebiegają po wszystkich atomach, a rozproszenia są na parach liczonych “każdy z każdym” (cztery typy par: , , oraz , a więc także przypadek “atom sam ze sobą”). Dla przypadku dwóch atomów z rys. 3.2, mielibyśmy sumę czterech rozproszonych amplitud:
Korzystając z twierdzenia cosinusów55 5 przepiszemy to jako:
Człony z sinusami upraszczają się, a każdy element sumy będzie zawierał wyraz . Wracając do ogólnego przypadku wielu atomów mamy więc:
czyli wyjściową amplitudę fali padającej pomnożoną przez pewien niezależny od czasu czynnik ją modulujący. Wartość czynnika zależy od kierunku obserwacji fali rozproszonej oraz od pozycji obiektów rozpraszających względem siebie . Ponadto, łącznie dla wszystkich orientacji , wartość powinna sumować się do . Zgodnie z przepisem na natężenie, wykreślamy z wyrażenia na amplitudę (3.1.2) człon i podnosimy do kwadratu moduł amplitudy . Oznaczając natężenie fali padającej jako , a natężenie fali rozproszonej jako , mamy:
W powższym wyrażeniu oznacza absolutne natężenie promieniowania padającego, zaś - absolutne natężenie promieniowania rozproszonego. W praktyce to liczba fotonów (“na sztuki”) padających na próbkę, zaś to liczba fotonów (też “na sztuki”) rozproszonych przez próbkę. Prawdopodobieństwo oddziaływania fotonów z daną próbką jest stałe (nie zależy od liczby fotonów), więc zwiększając (np. dwa razy), proporcjonalnie zwiększamy także . Dzieląc obie strony wyrażenia (3.1.2) przez (czyli normując do natężenia promieniowania padającego) otrzymamy wyrażenie na względne natężenie rozproszone:
| (3.14) |
gdzie jest częścią (ułamkiem) natężenia padającego, rozproszonego w kierunku określonym przez wektor rozpraszania .
W dyfrakcji, spektroskopii, a nawet w zwykłej fotografii najważniejsza jest nie tyle znajomość absolutnego natężenia (wartości liczbowej) poszczególnych pixeli, ile względnej relacji między pixelami obrazu. Na przykład, dla zrozumienia treści zdjęcia nie jest ważne czy dany pixel ma wartość rzędu tysięcy czy milionów (czy naświetlamy obraz silnym światłem w słoneczny dzień czy słabszym w pochmurny), ale ważne czy punkty ciemniejsze i jaśniejsze są w prawdziwych proporcjach i tworzą wyraźny, kontrastowy obraz z dużą ilością szczegółów66 6 Zaniedbanie natężeń absolutnych na rzecz względnych jest wybiegiem mającym na celu jak największe uproszczenie teorii. Uważny Czytelnik zauważy, że tutaj oraz w dalszych wyprowadzeniach operujemy tylko ciągłymi funkcjami natężenia, nic sobie nie robiąc z kwantowej natury promieniowania. Natężenia absolutne są ważnym elementem wiarygodności pomiaru (odstęp sygnału od szumu) i będą musiały pojawić się z powrotem w czasie szacowania błędów pomiarowych dyfrakcji.. Z tego powodu wyrugowanie z naszych wzorów natężeń absolutnych po pierwsze upraszcza te wzory, a po wtóre zbliża nasz opis do rzewczywistości doświadczalnej, w której najczęściej nie znamy natężeń absolutnych a tylko względne (wartości w ogóle się nie mierzy).
W celu dalszego uproszczenia wyrażenia (3.14) można pominąć symbole sumowania (notacja Einstein’a77 7 Podobno (przekaz ustny, nie znalazłem potwierdzenia pomimo prawie 90 sekund googlowania) nie tyle Einstein’a, ile jego drukarza. Zauważył on, że nawet przy braku znaku sumowania formuła jest dalej jednoznaczna. Za to o wiele krótsza i czytelniejsza.), pamiętając, że indexy przebiegają po wszystkich oświetlonych atomach próbki. W takim zapisie natężenie promieniowania rozproszonego na grupie atomów, których względne położenia dane są wektorami , obserwowane w kierunku będzie:
| (3.15) |
gdzie , są atomowymi czynnikami rozpraszania atomów oraz .
3.2 Równanie Debye’a
Możliwych odległości i orientacji między parami atomów jest w makroskopowych próbkach nanomateriałów zbyt dużo, żeby wyrażenie (3.15) było praktyczne. Możliwe do obserwacji są natężenia od wielkich grup atomów, najlepiej w uśrednionych orientacjach: nanomateriały (np. nanoproszki, żele, nanoceramiki, stopy, szkła, fulereny, itp.) w swoich próbkach objętościowych najpewniej będą “promować” przypadkowe orientacje cegiełek (np. nanokryształów) je budujących, a więc i par atomowych wewnątrz tych cegiełek. Dlatego korzystniejsze byłoby uzyskanie natężenia uśrednionego po wszystkich możliwych orientacjach:
| (3.16) |
Uśrednienie natężenia emitowanego w kierunku przestrzennym przez parę atomów o czynnikach atomowych, odpowiednio i , odległych od siebie o osiągniemy poprzez wycałkowanie po pełnym kącie bryłowym natężenia dla orientacji i unormowanie do powierzchni sfery całkowania. Zwykle całka pewnej funkcji we współrzędnych sferycznych wygląda następująco:
| (3.17) |
gdzie jest elementem powierzchni sfery o promieniu , po której całkujemy. W tak wybranym układzie współrzędnych (rys. 3.3) całkę po można porównać do pełnego obrotu Ziemi wokół własnej osi (dzień/noc), zaś całkę po do pochylania osi Ziemi (pory roku) aż do zamiany biegunów miejscami. W naszym przypadku całkowanie po w ogóle nie występuje, ponieważ chcemy uśredniać tylko orientacje, ignorując długość wektora (całka jest więc powierzchniowa, nie objętościowa). Ponieważ chcemy uśredniać, a nie sumować, podzielimy wynik całkowania przez powierzchnię sfery dopisując czynnik (podobnie jak licząc średnią długość zapałki, po zsumowaniu długości wszystkich, dzielimy wynik przez ich liczbę). Całka po sprowadza się do pomnożenia wyniku przez , ponieważ iloczyn skalarny zależy tylko od kąta (tak jak pora roku zależy tylko od nachylenia osi Ziemi, a nie zależy od godziny zegarowej, czyli obrotu wokół tej osi), rys. 3.3.
Wykonując całkę po wszystkich orientacjach, czyli przechodząc od wielkości wektorowych do ich modułów , przechodzimy od krystalografii monokrystalicznej do proszkowej. Kierunki trójwymiarowe znikają, orientacje konkretnej pary atomów w konkretnie zorientowanym krysztale zastępują miliony identycznych par zorientowanych równomiernie w każdym możliwym kierunku (proszek idealny). Orientacje trójwymiarowego wektora rozpraszania , a więc plamki na kliszy z dyfrakcji monokrystalicznej, zastępują tzw. pierścienie Debye’a-Scherrer’a, czyli koncentryczne jasne okręgi na kliszy, o promieniu odpowiadającym modułowi . Odtąd skalar będzie oznaczał moduł wektora rozpraszania, jednak dla zwięzłości dalej będziemy go nazywać po prostu “wektorem rozpraszania”, bo nie powoduje to nieporozumień. Podobnie, wektor łączący oba rozpraszające atomy przestaje mieć orientację (całka ją “zjada”), ale zachowuje swoją długość , czyli odległość między tymi atomami.
Przechodząc od do skalarów wykonujemy iloczyn skalarny . Czynnik typu możemy uśrednić następująco:
Czynniki oraz skracają się. Podstawmy teraz . W takim razie , dolna granica całkowania zmieni się: , zaś górna: . Dostaniemy:
Tak więc natężenie obserwowane pod kątem odpowiadającym wektorowi rozpraszania pochodzące od pary atomów o uśrednionej orientacji będzie:
| (3.18) |
Natężenia są addytywne, wiec dla realnego układu wielu atomów dowolnego rodzaju (krystalicznego, bezpostaciowego, cieczy, gazu, itp.) o czynnikach atomowych , obserwowane natężenie będzie:
| (3.19) |
Sumy w powyższym wyrażeniu przebiegają po wszystkich parach atomów oświetlonych wiązką, łącznie z elementami typu , które odpowiadają rozproszeniu na pojedynczym atomie (tworzy on “parę” sam ze sobą). Osobliwie, w takim przypadku , zerują się licznik i mianownik. Dlatego trzeba tu pamiętać, że funkcja dla przyjmuje wartość .
Wyrażenie (3.19) jest nazywane wzorem Debye’a. Podał je w 1915 roku [6] holendersko-niemiecko-amerykański fizyk i chemik Piotr (Peter) Debye (1884-1966), rys. 3.4. Jest to jedno z najsilniejszych i jednocześnie najogólniejszych twierdzeń w teorii dyfrakcji.
 |
 |
 |
Fotografia: Copyright by Museum Boerhaave: ’vrij beschikbaar voor publicatie / freely available for publication’
3.3 Równanie Debye’a dla kryształów, warunek Bragg’a
W roku 1915 Piotr Debye pokazał [6], że natężenie promieniowania rozproszonego przez dowolny88 8 zarówno krystaliczny jak amorficzny układ atomów, dane w jednostkach elektronowych, wynosi:
| (3.20) |
gdzie i są atomowymi czynnikami rozpraszania odpowiednich atomów oraz ; jest wektorem rozpraszania, zaś odległością pomiędzy tymi atomami. Natężenie jest uśrednione po wszystkich orientacjach przestrzennych. Wzór Debye’a użyty dla układu atomów tworzących pojedynczy krystalit, dostarcza w efekcie dyfraktogram proszku złożonego z takich właśnie, przypadkowo zorientowanych krystalitów.
Rozważmy substancję składającą się z rodzajów atomów, np. i w przypadku , (). Zbiór wszystkich możliwych par atomów można podzielić na podzbiorów par tego samego typu99 9 Oczywiście, pary i , np. i są równoważne z punktu widzenia wzajemnych odległości międzyatomowych w parze, tak więc zamiast podzbiorów można by utworzyć tylko . Jednak dla prostoty zostaniemy przy ., np. , , i . Możemy indeksować wszystkie typy par jako , gdzie opisuje skład pary, np. , , i .
Teraz równanie Debye’a (3.20) można przepisać:
| (3.21) |
gdzie pierwsze dwie sumy są po wszystkich typach par, dwie ostatnie - po wszystkich parach tego samego typu. Ponieważ wielu1010 10 szczególnie w kryształach parom w wewnętrznej sumie odpowiada ta sama odległość międzyatomowa , wygodnie jest skonsolidować wszystkie odległości przez wprowadzenie histogramu odległości międzyatomowych, czyli Funkcji Korelacji Par (Pair Correlation Function, ), rys. 3.5:
| (3.22) |
gdzie jest deltą Diraca.
a)
|
b) 
|
Zmodyfikowane równanie Debye’a (3.21) przyjmuje postać:
lub:
| (3.23) |
gdzie jest wielkością (np. średnicą) krystalitu. Operując funkcją korelacji par unormowaną do jedności, należy (3.23) dodatkowo pomnożyć przecz całkowitą liczbę par atomów w krystalicie. Ponieważ:
całka w (3.23) jest transformatą furierowską, Fourier Transform , a dokładniej: transformatą sinusów funkcji :
| (3.24) |
Korzystając z (3.24) można obliczyć dyfraktogram proszkowy dowolnego zbioru atomów bez względu na jego strukturę, uporządkowanie czy skład, zarówno w zakresie rozpraszania niskokątowego () jak i dyfrakcji bragowskiej\nomenclatureKąt Bragg’akąt pomiędzy płaszczyzną krystaliczną a padającą na nią wiązką promieni X, pod którym nastąpi pozytywna interferencja, tzn. fale odbite od wszystkich atomów płaszczyzny znajdą się w fazie i dzięki temu nie zginą., rys. 3.6. Część niskokątowa krzywej zawiera charakterystyczne oscylacje o okresie , gdzie jest wielkością ziarna. Biorą się one z nadreprezentacji odległości odpowiadających wielkości ziarna, przy całkowitym braku odległości niewiele większych. Mamy tu do czynienia ze sztucznym modelem proszku składającego się z ziaren identycznej wielkości (proszek monodyspersyjny), podczas gdy w rzeczywistości zawsze mamy do czynienia z dyspersją rozmiarów ziaren (o czym mowa w dalszej części).
a)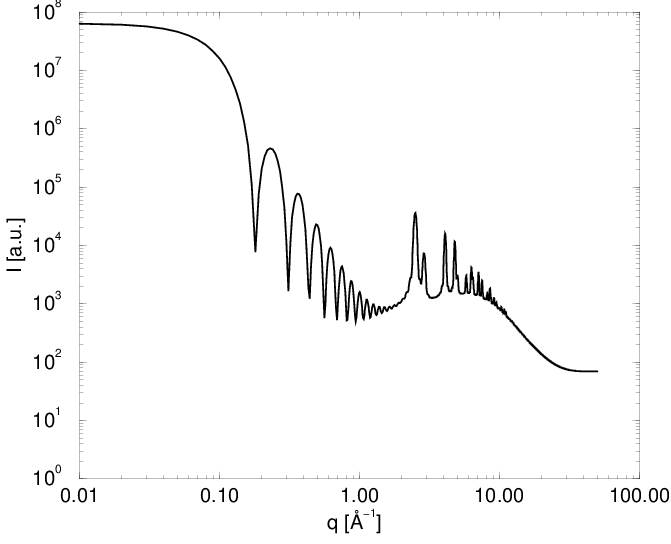
|
b)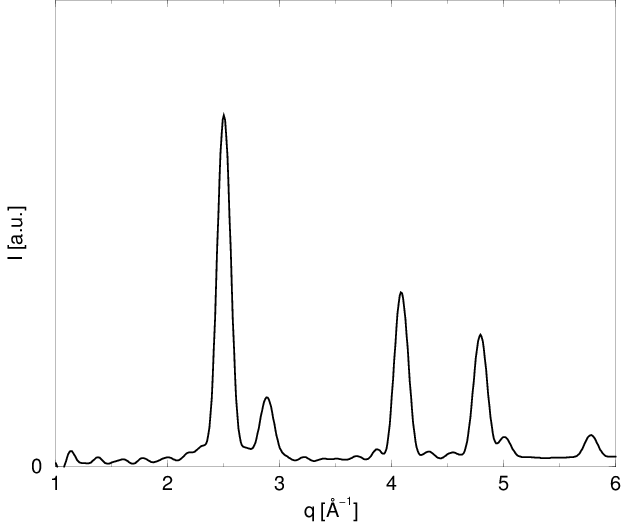
|
Korzystając z 2.1, wzór Debye’a można przepisać do postaci:
Definiuje on obserwowaną krzywą dyfrakcyjną jako transformatę furierowską iloczynu dwóch funkcji: rozkładu radialnego struktury podzielonego przez i dystrybucji kształtu krystalitu . Na podstawie twierdzenia Stokes’a (transformata iloczynu funkcji jest splotem transformat tych funkcji określonym w przestrzeni odwrotnej) można otrzymać:
| (3.25) |
W tej postaci wzór Debye’a jest splotem dwóch funkcji: transformaty i transformaty dystrybucji kształtu krystalitu . Zarówno jak i są funkcjami rzeczywistymi i interesujące są tylko części cosinusowe ich transformat. Rozwijając pierwszą z transformat dostajemy:
Szereg (LABEL:mathed:FFT(RDF/r)_1) jest rozbieżny o ile:
| (3.27) |
czyli o ile spełniony jest warunek Bragg’a. Jest on zaś spełniony dla przeliczalnego zbioru wartości wektora rozpraszania , wyznaczającego położenia refleksów bragowskich. Z kryterium całkowego zbieżności szeregów wiadomo, że szereg typu jest rozbieżny do , więc suma szeregu (LABEL:mathed:FFT(RDF/r)_1) dla wynosi:
| (3.28) |
Dla wartości wektora rozpraszania niespełniających warunku Bragg’a, suma szeregu (LABEL:mathed:FFT(RDF/r)_1) jest skończona, a więc zaniedbywalna w porównaniu do (3.28). Wynika stąd, że transformata jest szeregiem (“grzebieniem”) funkcji delta Diraca zlokalizowanych w tych miejscach na dyfraktogramie, które odpowiadają położeniom linii bragowskich, czyli wartościom wektora rozpraszania . Ów “grzebień” refleksów, spleciony na mocy (3.25) z transformatą dystrybucji kształtu krystalitu , czyli profilem linii dyfrakcyjnej, daje dyfraktogram proszkowy.
3.4 Proszki monodyspersyjne
Metody stosowane dotychczas. Tradycyjna, nienanokrystaliczna, dyfrakcja proszkowa opisywana jest w oparciu o kinematyczną teorię dyfrakcji Laue’go. Zakłada ona brak ugięć wielokrotnych oraz stałość absorpcji w krysztale. Założenia te są dobrze spełnione dla nanokryształów, mających często formę proszków.
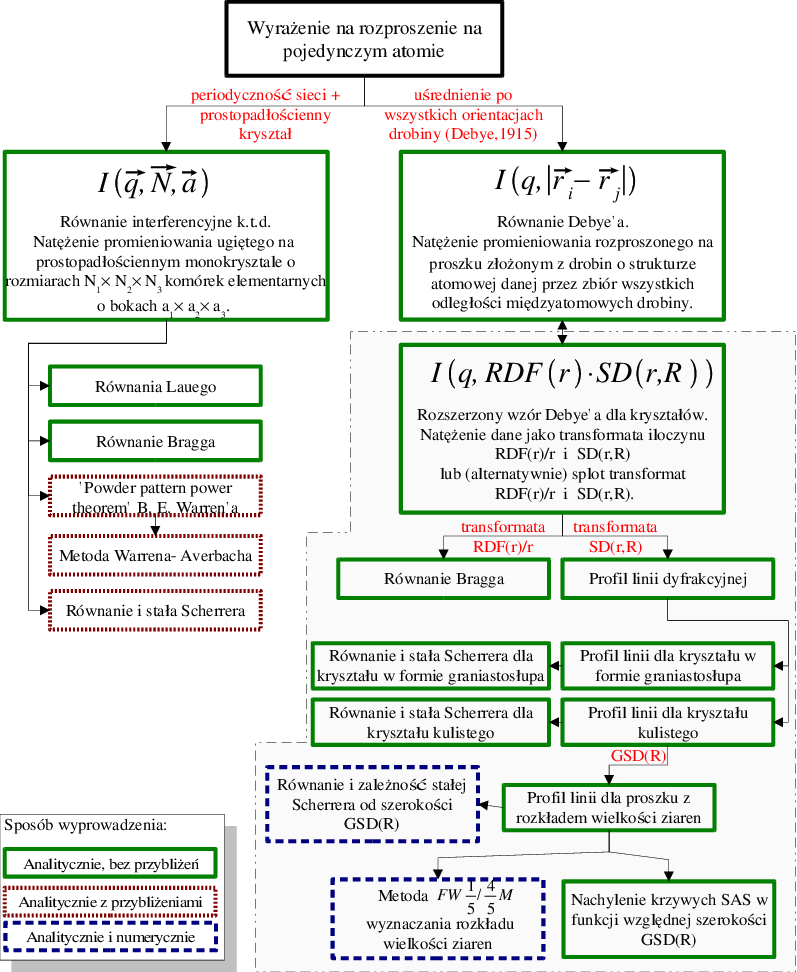
Przyjmując, że wszystkie krystality w proszku są identyczne, tzn. mają takie same rozmiary i kształty, można wydatnie uprościć matematyczny opis dyfrakcji proszkowej. Jest to podejście standardowo używane w teorii dyfrakcji. Zasadnicze, interferencyjne równanie teorii kinematycznej (3.1) (patrz np. wyrażenie (3.48) w pracy [58] lub (3.6) w pracy [55]) zostało wyprowadzone dla natężenia promieniowania rozproszonego na monokrysztale a więc przy założeniu periodycznej struktury atomowej przyjmując ponadto prostopadłościenny kształt kryształu (lewa gałąź diagramu przedstawionego na rys. 3.7). Pomimo tego, równanie interferencyjne jest punktem wyjścia tradycyjnych metod analizy proszkowych (a więc nie monokrystalicznych) danych dyfrakcyjnych, takich jak metoda Warren’a-Averbach’a lub metoda Scherrer’a. Na rys. 3.7 zestawiono najważniejsze metody analizy dyfrakcji promieniowania rentgenowskiego rozwinięte w ramach kinematycznej teorii dyfrakcji, zaznaczając ich wzajemne powiązania.
Jak wspomniano, równanie Debye’a jest “czysto proszkowe”, tzn. zakłada losową orientację drobiny. Dysponując równaniem Debye’a w wersji dla kryształów (§3.2), łatwo wyprowadzimy najważniejsze wielkości teorii kinematycznej (proszki monodyspersyjne), pokazując przy okazji zgodność obu podejść. W dalszej części (§3.5) do tak wyprowadzonych wielkości dodamy rozkład wielkości ziaren, żeby uzyskać bardziej funkcjonalną teorię - nadającą się dla szerokiej klasy realnych nanoproszków.
3.4.1 Profil linii i stała Scherrer’a dla kryształów prostopadłościennych
 |
 |
 |
Dla kryształów, których przekrój jest stały na całej ich długości (rys. 3.8), np. w kształcie graniastosłupa, dystrybucja kształtu jest odcinkiem (rys. 3.9a) i dana jest wzorem:
| (3.29) |
gdzie jest rozmiarem (tutaj: długością) kryształu. Posiada ona analityczną transformatę Fourier’a, czyli profil linii dyfrakcyjnej , w postaci (rys. 3.9b):
| (3.30) |
gdzie jest rozmiarem (tutaj: długością) krystalitu zaś jest wektorem rozpraszania. Natężenie w maksimum profilu jest proporcjonalne do rozmiaru krystalitu:
| (3.31) |
Porównując wyrażenie na profil linii dyfrakcyjnej (3.30) z połową wysokości tej linii (3.31) otrzymujemy:
Po prostych przekształceniach dostajemy:
Podstawiając i zaniedbując mianownik mamy:
| (3.32) |
Powyższe równanie jest równaniem przestępnym, którego jedyny nieujemny pierwiastek, , można wyznaczyć graficznie (rys. 3.9c) lub numerycznie z dowolną precyzją.
 |
a)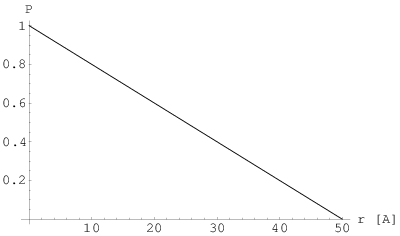
|
b)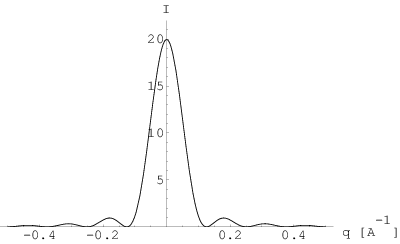
|
c)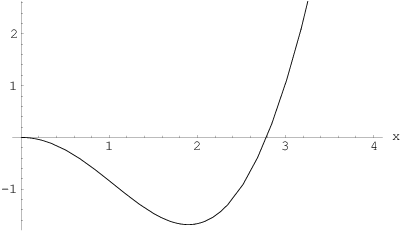
|
 |
d)
|
e)
|
f)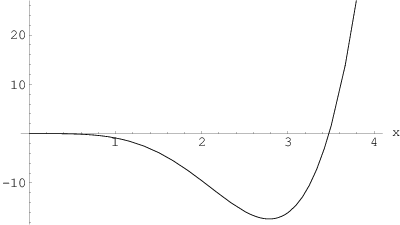
|
Wynosi on:
Po ponownym podstawieniu otrzymujemy zależność połowy szerokości profilu linii od wielkości kryształu :
Pamiętając, że szerokość połówkowa (szerokość połówkowa to szerokość obu połówek profilu linii mierzona w połowie jego wysokości), otrzymujemy równanie Scherrer’a:
| (3.33) |
gdzie jest stałą Scherrer’a. Z rozwiązania równania przestępnego (3.32) i równania Scherrer’a (3.33) wynika wartość stałej Scherrer’a dla kryształów prostopadłościennych:
| (3.34) |
3.4.2 Profil linii i stała Scherrer’a dla kryształów kulistych
Kryształy nie wykazujące wyraźnej anizotropii kształtu mogą być traktowane jako kuliste. To samo dotyczy kryształów o kształtach nieregularnych lub anizotropowych lecz w losowych kierunkach (np. rozdrobnionych monokryształów kubicznych) oraz wielościanów foremnych o dużej liczbie ścian (rys. 3.10).
a)
|
b)
|
c)
|
d)
|
e)
|
f)
|
g)
|
We wszystkich wspomnianych przypadkach dystrybucja kształtu kuli jest bardzo dobrym przybliżeniem dystrybucji kształtu kryształu. Dystrybucja kształtu kuli (rys. 3.9d) jest znana w postaci analitycznej:
oraz posiada analityczną transformatę Fourier’a, czyli profil linii dyfrakcyjnej proszku złożonego z identycznych krystalitów w kształcie kuli (rys. 3.9e):
| (3.35) |
gdzie jest średnicą krystalitów zaś jest wektorem rozpraszania. Natężenie maksimum profilu wynosi:
| (3.36) |
Porównując wyrażenie na profil linii dyfrakcyjnej (3.35) z połową wysokości tej linii (3.36) otrzymujemy:
Po prostych przekształceniach dostajemy:
Wprowadzając nieznikającą zmienną bezwymiarową i zaniedbując mianownik mamy:
| (3.37) |
Powyższe równanie jest przestępne i posiada pojedynczy dodatni pierwiastek, , który można znaleźć graficznie (rys. 3.9f) lub numerycznie z dowolną skończoną precyzją. Wynosi on:
Po ponownym podstawieniu otrzymujemy zależność połowy szerokości profilu linii od wielkości kryształu :
Pamiętając, że szerokość połówkowa , dostajemy równanie Scherrer’a:
| (3.38) |
gdzie jest stałą Scherrer’a. Z rozwiązania równania przestępnego (3.37) i równania Scherrer’a (3.38) wynika wartość stałej Scherrer’a dla kryształów w kształcie zbliżonym do kuli:
| (3.39) |
3.4.3 Prawo Porod’a dla kryształów kulistych
Dalsza analiza profilu linii dyfrakcyjnej (3.35):
może prowadzić do ustalenia, w jakich warunkach profil linii maleje jak , czyli spełnia prawo Porod’a. Aby to ustalić przepiszemy licznik (3.35), podstawiając jak poprzednio i zaniedbując stałe:
| (3.40) |
Analiza przebiegu powyższej funkcji (rys. 3.11a) pokazuje, że jest ona przedziałami wolnozmienna. Istotnie, jej pochodna (rys. 3.11b):
| (3.41) |
znika dla , . Tak więc w otoczeniu , możemy traktować licznik (3.35) jako stały i zapisać wyrażenie na profil linii dyfrakcyjnej w postaci:
| (3.42) |
czyli jako prawo Porod’a.
a)
|
c)
|
|---|---|
b)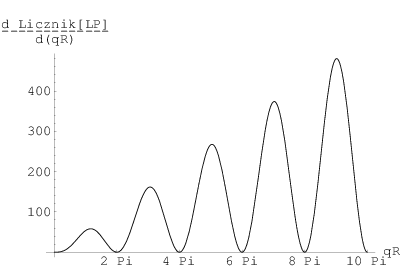
|
d)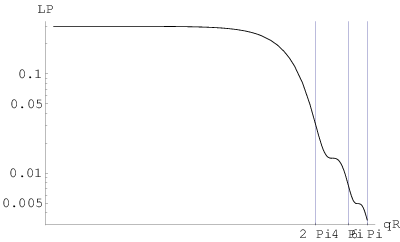
|
e)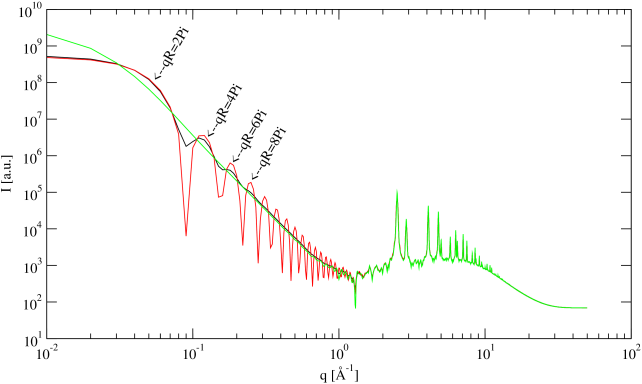
|
|
Warunek jest ważny zarówno dla bragowskich linii dyfrakcyjnych jak i profilu rozpraszania niskokątowego, gdyż teoria Debye’a nie czyni żadnych założeń co do struktury atomowej rozpraszających obiektów. Jednak mierzone w obu tych przypadkach natężenia różnią się typowo o 3-4 rzędy wielkości co zmusza do ich osobnej interpretacji.
3.4.3.1 Profil linii bragowskiej
Pierwszy obszar profilu linii bragowskiej, gdzie spełnione jest prawo Porod’a () znajduje się w końcowej części ramienia tego profilu w skali liniowej (rys. 3.11c). Natężenie linii w tym miejscu stanowi około jej maksimum i może być wykorzystane do określenia wielkości ziarna o ile nie istnieją przeszkody w postaci zniekształceń profilu w tym miejscu (np. inne maksima, błędy ułożenia, itp.). Niestety, w praktyce takie przeszkody występują często (dla opisywanych dalej przykładów nanokrystalicznych , i - zawsze). Kolejne “porodowskie” obszary profilu ( ) znajdują się daleko od maksimum linii bragowskiej i ich natężenia są na poziomie szumów.
3.4.3.2 Profil niskokątowy
W skali log-log (rys. 3.11d i e) na profilu rozpraszania niskokątowego widać zwykle kilka lub kilkanaście oscylacji odpowiadających warunkowi dla kolejnych . Oscylacje są obecne tylko w przypadku proszku monodyspersyjnego (ziarna o tym samym rozmiarze). W realnych sytuacjach proszków polidyspersyjnych (ziarna o różnych rozmiarach) oscylacje uśredniają się i widać zbocze o nachyleniu . W praktyce nie sposób więc zlokalizować żadnego z miejsc, gdzie spełniony jest warunek za wyjątkiem , gdzie zagina się prosta . Stanowi to podstawę wyznaczania rozmiaru ziaren z profili rozpraszania niskokątowego dla proszków o niezbyt szerokim rozkładzie wielkości ziaren.
3.5 Proszki polidyspersyjne
Alternatywnym do równania interferencyjnego K.T.D podejściem do opisu dyfrakcji promieniowania rentgenowskiego jest równanie Debye’a [6]. Równanie to umożliwia obliczenie dyfraktogramu proszkowego w zakresie kąta pełnego jedynie w oparciu o znajomość rozkładu odległości międzyatomowych w rozpraszającej drobinie. Teoria ta nie wymaga periodyczności sieci krystalicznej, zakłada zaś przypadkową orientację drobiny1111 11 Ponieważ tutaj “drobiną” będzie zawsze nanokryształ, będziemy używać tego drugiego określenia. Dodatkowe (z puntu widzenia teorii Debye’a) założenie o periodyczności sieci drobiny zostało wykorzystane przy wyprowadzaniu rozszerzonej wersji wzoru Debye’a dla kryształów.; ponadto przyjmuje, podobnie jak teoria Laue’go, brak ugięć wielokrotnych oraz stałość absorpcji. Założenie dotyczące przypadkowej orientacji drobin (krystalitów) pokrywa się z fizyczną rzeczywistością dyfrakcji proszkowej, będąc zaletą teorii i w niczym nie ograniczając jej ogólności. Korzystając ze wzoru Debye’a dostaje się więc natężenie promieniowania rozproszonego na proszku złożonym z identycznych drobin o dowolnym kształcie i strukturze atomowej.
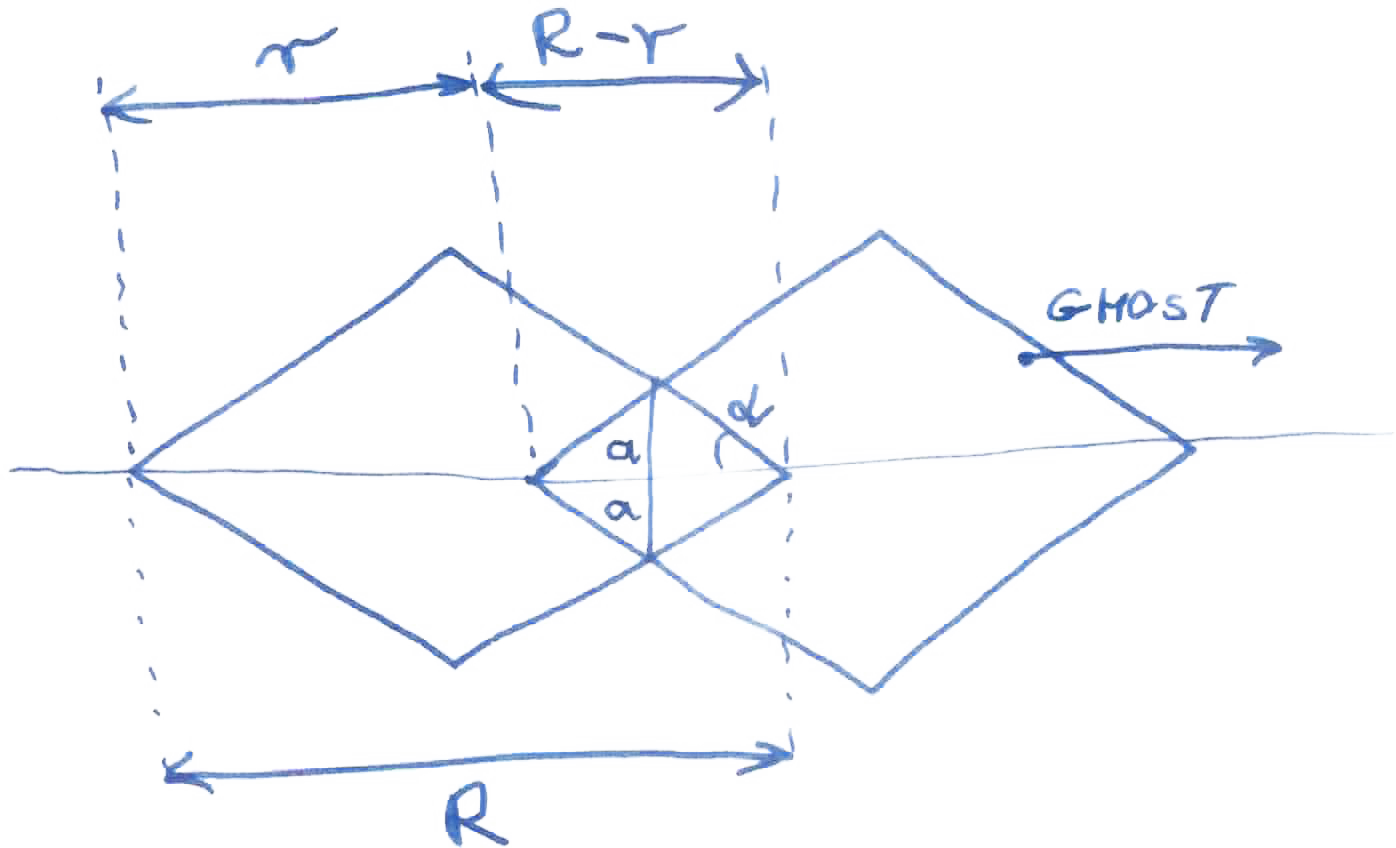
Na początku lat czterdziestych ubiegłego wieku Stokes i Wilson podali związek pomiędzy szerokością integralną linii bragowskich a pewną funkcją, obliczaną jako objętość części wspólnej krystalitu i jego własnej kopii (“ducha” lub “cienia” krystalitu, ang. shadow) przesuniętej względem oryginału w kierunku rozpraszania [51], rys. 2.2. Korzystają oni z własności tej funkcji chociaż, jak piszą, “nie jest łatwo dostrzec jej fizyczne znaczenie”. W latach pięćdziesiątych i sześćdziesiątych XX-go wieku opublikowano prace wiążące transformatę furierowską profilu linii dyfrakcyjnej z funkcją Stokes’a i Wilson’a [56, str.41][13][57]. Guinier pisze o tej funkcji, że “wykazuje własności analogiczne do funkcji będącej transformatą Fouriera profili linii Debye’a-Scherrer’a poszerzonych w efekcie małego rozmiaru kryształu (Bertaut [3])” oraz że “nie ma (ona) intuicyjnego związku z formą drobiny” [13, str.12]. W latach późniejszych, korzystając z własności transformaty funkcji Stokes’a i Wilson’a, obliczono profile linii dyfrakcyjnych dla krystalitów o niektórych kształtach (np. [26][53]).
W dalszym ciągu spróbujemy rozwinąć tradycyjną teorię Debye’a oraz połączyć ją z podejściem Stokes’a i Wilson’a oraz Bertaut i Guinier. Korzystając z równania Debye’a dla periodycznej sieci krystalicznej wyprowadzimy, bez dodatkowych założeń, wyrażenia wiążące kształt i rozmiar (nano)krystalitów z profilem linii dyfrakcyjnej proszków polidyspersyjnych, przy czym rolę funkcji Stokes’a i Wilson’a spełni w tym podejściu dystrybucja kształtu kryształu, posiadająca przejrzystą interpretację fizyczną.
3.5.1 Rozkład wielkości ziaren proszku
Aby otrzymać profil linii dyfrakcyjnej pochodzącej od proszku zawierającego ziarna o różnych wielkościach, należy scałkować wyrażenie na profil linii z żądanym rozkładem wielkości ziaren (). Na przykład, dla ziaren zbliżonych do kuli, należałoby obliczyć całkę z (3.35):
| (3.43) |
Postać samej funkcji rozkładu wielkości ziaren podyktowana jest zazwyczaj mechanizmem syntezy proszku. Najczęstszym wyborem jest rozkład log-normalny. Niestety, wyrażenie (3.43) jest niecałkowalne analitycznie dla szerokiej klasy asymetrycznych krzywych dzwonowych w tym również dla rozkładu log-normalnego. Całka (3.43) istnieje jednak w postaci analitycznej dla potęgowo-wykładniczego rozkładu wielkości ziaren (2.5). Rozkład wykładniczo potęgowy (rys. 2.5) jest analogiczny do rozkładu Poissona, jednak zmienna ma tu charakter ciągły. Z punktu widzenia zastosowań praktycznych jest on też na tyle podobny do rozkładu log-normalnego, że może być traktowany jako jego zamiennik, rys. 2.7. Unormowany rozkład (2.5) ma postać:
| (3.44) |
Średnia wielkość ziarna (moment rzędu 1) powyższego rozkładu wynosi:
| (3.45) |
moment drugiego rzędu:
| (3.46) |
zaś dyspersja:
| (3.47) |
Wygodnym parametrem rozkładu jest tzw. współczynnik zmienności (Coefficient of Variation, CV, ), będący miarą względnej szerokości rozkładu. Oblicza się go przez podzielenie dyspersji przez wartość oczekiwaną. Dla rozkładu wykładniczego wynosi on:
| (3.48) |
Parametry i rozkładu (2.5) powiązane są z jego wartością oczekiwaną i dyspersją w następujący sposób:
| (3.49) | |||||
| (3.50) |
Parametr (a dokładnie: ) może być traktowany jako miara względnej szerokości rozkładu (3.44). Duża wartość oznacza rozkład wąski zaś mała - szeroki. Ostatnie dwa wyrażenia pozwalają na przepisanie rozkładu (3.44) z użyciem parametrów i posiadających bezpośrednią interpretację fizyczną zamiast i :
| (3.51) |
gdzie jest średnią ważoną rozkładu, czyli średnią wielkością ziarna w proszku wyrażoną w Å. jest dyspersją rozmiarów ziaren, czyli szerokością rozkładu, również wyrażoną w Å. Rozkład wielkości ziaren dany przez (3.51) przypomina kształtem rozkład log-normalny i może być z powodzeniem traktowany jako jego funkcjonalny odpowiednik, rys. 2.7. Maksimum rozkładu (3.51) znajduje się w:
| (3.52) |
czyli najliczniej występujące ziarna mają średnicę nieco mniejszą niż średnia wielkość ziarna w proszku.
3.5.2 Dystrybucja kształtu wielościanów
Jak pokazano w §3.4.1, dystrybucja kształtu prostopadłościanu “wyciąganego” równolegle do którejś z jego osi, a więc w kierunku czołowym (rys. 2.6a), wynosi:
| (3.53) |
podczas gdy powierzchnia przekroju całego krystalitu jest:
| (3.54) |
skąd dystrybucja kształtu (powierzchnia części wspólnej unormowana do całości):
| (3.55) |
Jak widać, kąt występuje w tym samym kontekście zarówno w formule na część wspólną jak i na całość krystalitu i skraca się. Podobnie jest z innymi parametrami kształtu (np. grubością krystalitu, którą tu celowo pominięto). Łatwo pokazać, że analogicznie będzie w przypadku wierzchołkowym (rys. 2.6c): parametr będzie miał wymiar powierzchni, będzie funkcją i znów skróci się podczas normowania do całości krystalitu, zaś dystrybucja kształtu wyniesie:
| (3.56) |
W ogólności, dystrybucje kształtu wielościanów wypukłych mają ogólną postać:
| (3.57) |
gdzie wykładnik w przestrzeni trójwymiarowej przyjmuje wartości 1, 2 lub 3, zależnie od kierunku:
-
•
dla kierunku czołowego
-
•
dla kierunku krawędziowego
-
•
dla kierunku wierzchołkowego.
Warto zauważyć, że prosta postać bierze się ze zniesienia parametrów szczegółowo opisujących postać krawędzi, tzn. kąta miedzy ścianami krystalitu w przypadku krawędziowym lub wielu kątów - w przypadku wierzchołkowym. Oznacza to, że (i) profil linii nie zależy od tych kątów oraz że (ii) w przestrzeni trójwymiarowej istnieją tylko trzy fundamentalne dystrybucje kształtu dla kryształów wielościennych1212 12 Dystrybucję kształtu dowolnego wielościanu wypukłego, np. dla ściętego prostopadłościanu, można otrzymać przez złożenie odpowiednich dystrybucji elementarnych (np. dla odcinka prostopadłościennego, a potem dla fragmentu ściętego).. W przypadku krystalitów w kształcie sześcianu, trzy fundamentalne kierunki mają proste przełożenie na indeksy Millera (hkl) linii dyfrakcyjnych:
-
•
kierunek czołowy () odpowiada liniom typu , ,
-
•
kierunek krawędziowy () odpowiada liniom typu , ,
-
•
kierunek wierzchołkowy () odpowiada liniom typu ,
gdzie jest liczbą naturalną.
3.5.3 Profil linii proszków polidyspersyjnych (wielościany)
Profil piku dyfrakcyjnego dla kryształów wielościennych jest transformatą Fourier’a ich dystrybucji kształtu (3.57) i można go zapisać jako:
| (3.58) |
gdzie symbol oznacza uogólnioną funkcję hypergeometryczną. Funkcja hypergeometryczna jest zdefiniowana jako szereg:
| (3.59) |
gdzie:
| (3.60) |
Symbol nazywamy symbolem Pochhammer’a.
Historia funkcji (lub szeregów) hypergeometrycznych sięga . Zajmowali się nimi Leonard Euler (1707-1783), Karol F. Gauss (1777-1855, czasem bywają nazywane jego nazwiskiem), Bernard Riemann (1826-1866) i inni. W postaci (3.59), szereg hypergeometryczny podał w 1828 roku Tomasz Clausen (1801-1885) dla i . Leonard Pochhammer (1841-1920) wprowadził powyższą notację. Została ona później zmodyfikowana przez Ernesta W. Barnes’a (1874-1953).
Pożytek z funkcji hypergeometrycznych polega na tym, że można przy ich pomocy wyrazić w jednolity sposób wszystkie funkcje elementarne, wiele stałych oraz funkcji specjalnych, np. , , . Można także, co istotne dla nas, zapisać w ten sposób profile pików dyfrakcyjnych. Ale chyba najistotniejsze, że całka na hypergeometrycznej funkcji profilu linii prowadząca do wyrażenia na profil linii dla proszków polidyspersyjnych:
istnieje dla rzeczywistych oraz rzeczywistych i dodatnich: średniego rozmiaru ziaren i dyspersji rozmiarów ziaren , co pokrywa się z fizycznymi więzami dla tych wielkości. Całka ta wynosi:
| (3.61) |
gdzie zaś . Przy zapewnieniu, że i są rzeczywiste i dodatnie (co już założyliśmy), istnieje także całka:
| (3.62) |
czyli powierzchnia całkowita profilu linii (natężenie integralne piku). Natężenie w maksimum linii () wynosi:
| (3.63) |
Szczególnie ciekawe są przypadki , czyli profile linii w przestrzeni trójwymiarowej. Chociaż wyrażenie (3.61) wygląda na pierwszy rzut oka dość nieprzystępnie, okazuje się, że szereg hypergeometryczny można rozwinąć i uprościć. Co więcej, po rozwinięciu pozostaną w nim tylko: stałe, funkcje elementarne, parametry rozkładu wielkości ziaren i wektor rozpraszania .
Po rozwinięciu szeregu hypergeometrycznego (3.61) dla i redukcji do postaci funkcji elementarnych, zapiszemy go jako profil linii polidyspersyjnego proszku dla reflexów w kierunkach czołowych:
| (3.64) |
Podobnie postąpimy z szeregiem (3.61) dla . Otrzymamy w ten sposób profil linii polidyspersyjnego proszku dla reflexów w kierunkach krawędziowych:
Analogicznie, dla , otrzymamy profil linii polidyspersyjnego proszku dla reflexów w kierunkach wierzchołkowych:
Warto zauważyć, że profil linii bez przeszkód istnieje w przestrzeniach więcej niż trójwymiarowych1313 13 Wzór na profil linii dla podajemy jako ciekawostkę. Zjawisko dyfrakcja najwyraźniej nie jest ograniczone wymiarami przestrzeni do . ():
Odpowiednie wyrażenia w jednostkach i są nieco dłuższe, ale składają się wyłącznie z funkcji elementarnych i można je bezpośrednio stosować, np. w programach fitujących. Podstawienie do (3.64) zależności (3.49) i (3.50) oraz wykonanie prostych przekształceń pozwala przejść od parametrów rozkładu wykładniczo-potęgowego () do parametrów fizycznych (). Profil linii polidyspersyjnego proszku dla reflexów w kierunkach czołowych, w jednostkach fizycznych oraz ma postać:
Powyższe wyrażenie ma wektor rozpraszania w liczniku i w mianowniku. Technicznie, może to spowodować osobliwość (błąd dzielenia przez zero) przy próbie obliczenia natężenia linii w jej centrum. Oczywiście, wyrażenie (3.5.3) jest jak najbardziej określone dla i na mocy (3.63) jego wartość wynosi tam . W razie trudności obliczeniowych, należy środek profilu obliczać osobno: dla jako wartość podstawiać , zaś wszędzie indziej wartość wyrażenia (3.5.3).
Profil linii polidyspersyjnego proszku dla reflexów w kierunkach krawędziowych, w jednostkach fizycznych oraz ma postać:
Podobnie jak poprzednio, w razie trudności obliczeniowych, należy środek profilu obliczać osobno: dla jako wartość podstawiać , zaś wszędzie indziej wartość wyrażenia (3.5.3).
Profil linii polidyspersyjnego proszku dla reflexów w kierunkach wierzchołkowych, w jednostkach fizycznych oraz ma postać
Jak poprzednio, w razie trudności obliczeniowych, należy środek profilu obliczać osobno: dla jako wartość podstawiać , zaś wszędzie indziej wartość wyrażenia (3.5.3).
3.5.4 Profil linii proszków polidyspersyjnych (ziarna kuliste)
Wyrażenie (3.43) na profil linii dyfrakcyjnej dla proszku z niezerową dyspersją wielkości ziaren kulistych wyrazimy dla prostoty najpierw w zmiennych i , podstawiając (3.44):
| (3.71) |
Całka (3.71) istnieje o ile wielkości , oraz są rzeczywiste i dodatnie, co jest spełnione ze względu na ich sens fizyczny. Po wykonaniu całkowania otrzymujemy:
W powyższym wzorze funkcje gamma Eulera występują w liczniku i mianowniku, dlatego można je uprościć. Najprostsza postać wyrażenia na profil linii dyfrakcyjnej proszku złożonego z kulistych ziaren z wykładniczo-potęgowym rozkładem wielkości jest:
Wyrażenie (3.5.4) składa się wyłącznie z funkcji elementarnych i może być wygodnie używane zarówno w obliczeniach numerycznych jak i do dalszych przekształceń symbolicznych. Natężenie linii w jej maksimum () można obliczyć przechodząc w (3.5.4) do granicy :
| (3.74) |
Powierzchnia piku (natężenie integralne) jest stała i wynosi:
| (3.75) |
Podstawienie do (3.5.4) zależności (3.49) i (3.50) oraz wykonanie prostych przekształceń pozwala przejść od parametrów rozkładu wykładniczo-potęgowego () do parametrów fizycznych (). Otrzymujemy tą drogą wyrażenie na profil linii dyfrakcyjnej proszku polidyspersyjnego jako funkcję i , mających bezpośrednią fizyczną interpretację, rys. 2.4a:
| (3.76) | |||||
Wyrażenie powyższe, będąc dokładnym odpowiednikiem (3.5.4), jest użyteczne jako wzór na profil linii dyfrakcyjnej proszku z rozkładem wielkości ziaren wyrażony w zrozumiałych jednostkach, ale jest od (3.5.4) dłuższe. Dlatego do przekształceń algebraicznych wykorzystywać będziemy raczej (3.5.4) niż (3.76) pamiętając o ich wzajemnej równoważności.
Powyższe wyrażenie ma wektor rozpraszania w liczniku i w mianowniku. Technicznie, może to spowodować osobliwość (błąd dzielenia przez zero) przy próbie obliczenia natężenia linii w jej centrum. Oczywiście, wyrażenie (3.76) jest jak najbardziej określone dla i na mocy (3.74) jego wartość wynosi tam . W razie trudności obliczeniowych, należy środek profilu obliczać osobno: dla jako wartość podstawiać , zaś wszędzie indziej wartość wyrażenia (3.76).
Wyrażenie (3.76) na proszkową linię dyfrakcyjną z rozkładem wielkości ziaren jest uogólnieniem wzoru (3.35) na linię dyfrakcyjną proszku monodyspersyjnego i w szczególnym przypadku zerowej dyspersji powinno się do niego upraszczać. Istotnie, przechodząc w (3.76) z dyspersją do granicy , dostajemy:
| (3.77) |
czyli wyrażenie monodyspersyjne.
3.5.5 - metoda Scherrer’a dla proszków polidyspersyjnych
W §3.4.1 i §3.4.2 aby wyprowadzić równanie Scherrer’a porównywaliśmy wyrażenie na profil linii dyfrakcyjnej z połową jego wysokości. Teraz postąpimy podobnie, z tym, że chwilowo zamiast stałej przed wysokością profilu postawimy współczynnik , któremu dopiero później przypiszemy wartości i . O proszku zakładamy, że jego rozkład wielkości ziaren jest postaci (3.44). Dla uproszczenia równań posługiwać się będziemy profilem linii (3.5.4) w zmiennych i , przechodząc na samym końcu do zmiennych i .
Porównując wyrażenie na profil linii dyfrakcyjnej proszku o niezerowej dyspersji rozkładu wielkości ziaren (3.5.4) z ułamkiem wysokości tej linii (3.74) otrzymujemy:
| (3.78) | |||||
Po przeniesieniu prawej strony równania ze zmienionym znakiem na lewą, sprowadzeniu do wspólnego mianownika i przegrupowaniu wyrazów dostajemy:
| (3.79) | |||||
Korzystając z faktu, że symbole oraz w powyższym równaniu zawsze występują parami, podstawimy otrzymując:
| (3.80) | |||||
Po zaniedbaniu mianownika i pierwszego członu , który zawsze jest różny od zera mamy:
| (3.81) | |||||
Powyższe równanie jest równaniem przestępnym z dwoma niewiadomymi ( traktujemy jako znane), którego rozwiązaniem jest krzywa . Równanie to można rozwiązać numerycznie traktując zmienne i jako parametry. Ciąg rozwiązań ze względu na parametr , dla dwóch ustalonych i tworzy monotoniczne krzywe i , pokazane na rys. 3.13 w postaci punktów. Postaci analitycznej tych krzywych niestety nie znamy. Można jednak wykreślić je dla szerokiego zakresu wartości , który całkowicie pokrywa interesujący przedział zmienności tego parametru1414 14 Parametr jest miarą względnej szerokości rozkładu wielkości ziaren. Praktyka pokazuje, że względna szerokość rozkładu na poziomie (wartość ) wystarcza już do traktowania proszku jako bezdyspersyjnego. Dlatego przy analizie profili linii dyfrakcyjnych proszków o niezerowej dyspersji rozkładu wielkości ziaren wystarczy ograniczyć się do .. Do tak wykreślonych krzywych można następnie dopasować arbitralnie wybraną funkcję elementarną i traktować ją dalej jako przybliżenie nieznanej analitycznie funkcji . Numeryczne rozwiązania równań (3.81) możemy przybliżyć funkcjami 1515 15 Próbowałem godzinami wielu różnych nieliniowo malejących funkcji ale właściwe rozwiązanie (cotangens pasuje idealnie, w pełnym zakresie zmienności, w każdym powiększeniu, z dokładnością do punktu ekranowego) odnalazł Ryszard Kutner (@fuw.edu.pl) po trzech sekundach obserwacji, za co uprzejmie dziekuję. otrzymując:
| (3.82) | |||||
| (3.83) |
Powyższe krzywe , stanowiące rozwiązania równania (3.81) wraz z ich dopasowaniem funkcją pokazano, odpowiednio, na rys. 3.13 a i b.
a)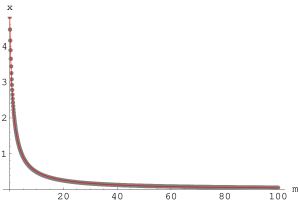
|
b)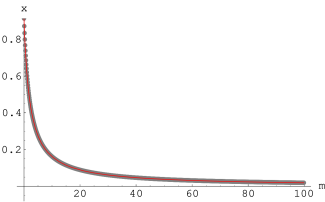
|
Pamiętając, że podstawiliśmy , znając rozwiązania i w postaci funkcji (3.82) i (3.83) oraz dysponując zmierzonymi szerokościami linii i , możemy zapisać układ równań:
| (3.84) |
którego dwie niewiadome i można łatwo obliczyć metodą
podstawiania. Następnie, korzystając z tożsamości (3.49)
i (3.50), można przejść ze zmiennych
do .
Wzory1616
16
Przypomnienie: operujemy tutaj w jednostkach wektora rozpraszania
. Szerokości linii dyfrakcyjnych
i wyrażone są więc w Å.
Odpowiednio, wielkości związane z rozmiarami w przestrzeni prostej
(np. i ) są wyrażone w Å.
Dysponując szerokościami i w stopniach
skali , można otrzymać ich wersje w skali wektora rozpraszania
podstawiając każdą z tych szerokości do wzoru (3.86)
w miejsce na średni rozmiar ziarna w proszku i dyspersję jako
funkcję mierzalnych wielkości i
proszkowej linii dyfrakcyjnej mają postać:
| (3.85) | |||||
gdzie pomocnicze współczynniki i wynoszą:
Dysponując szerokościami pików i pozycjami linii wyrażonymi w stopniach skali , można je przeliczyć do szerokości w skali wektora rozpraszania według wzoru:
| (3.86) | |||||
gdzie jest długością fali w [Å], jest szerokością linii1717 17 czyli kątową odległością między dwoma punktami dyfraktogramu. Mogą być one wzięte na dowolnej wysokości linii, niekoniecznie w połowie (Half) wysokości, stąd litera zamiast w symbolu . w stopniach skali , zaś stanowi połowę kąta określającego pozycję (środek) analizowanej linii. Wersje wzorów (3.85) w skali zapisano jako wyrażenie (2.9).
3.5.5.1 Funkcja Pearson VII w metodzie
Metoda wyznaczania rozkładu wielkości ziaren na podstawie pomiaru dwóch szerokości linii dyfrakcyjnej w i jej wysokości (§3.5.5) jest tylko tak precyzyjna jak wspomniane pomiary szerokości. Precyzję tę można podnieść poprzez dopasowanie do mierzonej linii dyfrakcyjnej dowolnej krzywej dzwonowej o minimum dwóch parametrach szerokości, pod warunkiem, że jakość dopasowania nie budzi zastrzeżeń. Często obecna w programach fitujących jest krzywa Pearson VII o postaci:
| (3.87) |
gdzie jest natężeniem w maksimum linii, - położeniem linii, zaś i parametryzują szerokość linii. Kładąc i i porównując wyrażenie (3.87) z oraz otrzymujemy równanie na szerokość krzywej Pearson VII w i jej wysokości:
| (3.88) |
Interesujące nas rozwiązania wynoszą:
| (3.89) | |||||
| (3.90) |
Wyrażenia te są funkcją parametrów i , będących bezpośrednim wynikiem działania programów fitujących (np. PeakFit). Można wstawić je do wzorów (3.85) na rozkład wielkości ziaren, otrzymując prostą praktyczną metodę na jego ustalenie, rys. 2.11.
3.5.6 Metoda Integral Breadth (uogólniona)
Natężenie integralne i natężenie w maksimum to jedne z najłatwiejszych do zmierzenia parametrów piku. Znając wartości obu tych natężeń można ustalić średni rozmiar krystalitów.
Rysunek 2.4 oraz wyrażenia (3.63) i (3.74) wskazują, że szczególną własnością pików proszków polidyspersyjnych jest zależność natężenia w ich maksimum od średniego rozmiaru ziarna przy braku zależności od dyspersji rozmiarów . Skoro natężenie integralne pików proszków polidyspersyjnych (wyrażenia (3.62) i (3.75)) dane w jednostkach elektronowych jest stałe i wynosi , zaś natężenia w maksimum są dane wyrażeniami (3.63) i (3.74), można porównać doświadczalnie zmierzone natężenie integralne piku i natężenie w maksimum piku do odpowiednich wyrażeń teoretycznych:
skąd średni rozmiar ziarna:
| (3.91) |
gdzie jest zmierzonym natężeniem integralnym piku, jest natężeniem zmierzonym w maksimum piku, jest rozmiarem średnim krystalitów danym w [Å], zaś jest parametrem zależnym od kształtu krystalitu i kierunku krystalograficznego. Parametr wynosi (rys. 2.6):
-
•
dla kryształów prostopadłościennych w kierunkach czołowych (np. ),
-
•
dla kryształów zbliżonych kształtem do kuli (niezależnie od kierunku),
-
•
dla kryształów prostopadłościennych w kierunkach krawędziowych (np. ),
-
•
dla kryształów prostopadłościennych w kierunkach wierzchołkowych (np. ).
W szczególnie użytecznym przypadku kryształów podobnych do kuli średni rozmiar ziarna wynosi:
| (3.92) |
Warto zauważyć, że natężenie integralne jest całką piku, czyli jego powierzchnią. W praktyce doświadczalnej mierzymy dyskretne natężenia w kolejnych kątach , a sumę tych dyskretnych natężeń także nazywa się natężeniem integralnym - mamy więc konflikt oznaczeń. Aby w przypadku dyskretnych natężeń otrzymać powierzchnię piku , należy pomnożyć sumę natężeń wszystkich zmierzonych punktów piku przez krok1818 18 Zakładamy, że krok jest stały, np. . Dla zmiennego kroku należy każde natężenie z osobna wymnożyć przez odpowiadający mu zakres kąta i dodać tak otrzymane cząstkowe powierzchnie do siebie. licznika przeliczonego do jednostek wektora rozpraszania według (3.86):
| (3.93) | |||||
| (3.94) |
gdzie jest natężeniem -tego z ogólnej liczby zmierzonych punktów piku, zaś to długość pojedynczego kroku goniometru w skali . Na przykład, dla piku zmierzonego w zakresie od do skali z krokiem mielibyśmy punktów i , oczywiście. Kąt jest (podzielonym przez 2) położeniem środka analizowanej linii w skali .
3.5.7 Prawo Porod’a dla proszków polidyspersyjnych
W §3.4.3 w przypadku proszków bez dyspersji rozmiarów stwierdziliśmy, że spełniają one prawo Porod’a, czyli w pewnych obszarach profil ich linii dyfrakcyjnych maleje jak . Znając analityczną postać wyrażenia (3.5.4) na profil linii dyfrakcyjnej proszku z rozkładem rozmiarów ziaren (Grain Size Distribution, ) ustalimy jak zależy nachylenie profilu linii od szerokości tego rozkładu. Używane w tym paragrafie pojęcie nachylenia profilu linii dyfrakcyjnej oznacza współczynnik nachylenia krzywej w skali log-log, czyli wykładnik krzywej w skali liniowej. Dyskutowane własności nachylenia mają zastosowanie głównie w odniesieniu do rozpraszania niskokątowego ().
Przyjmijmy, że posiadamy proszek o wykładniczo-potęgowym rozkładzie wielkości ziaren (3.44). Profil jego linii dyfrakcyjnej dany jest przez (3.5.4). Wyrażenie to umożliwia wyznaczenie nachylenia krzywej dyfrakcyjnej dla proszku w funkcji parametru (będącego miarą względnej szerokości , por. §3.5.1):
| (3.95) |
gdzie . Na rys. 3.14 wykreślono powyższą zależność w funkcji , czyli “monodyspersyjności” proszku (po przejściu od jednostek do ).
a)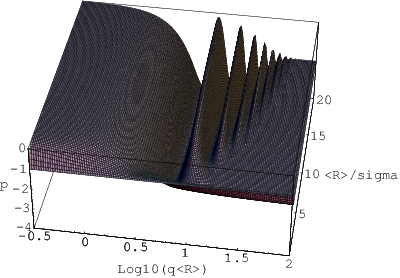
b) 
Dla dużych wartości (ziarna niemal identycznych rozmiarów) widoczne są oscylacje nachylenia krzywej niskokątowej. W miarę zwiększania się rozrzutu rozmiarów ziaren znikają oscylacje wyższych rzędów i w końcu (dla ) natężenie rozpraszania niskokątowego maleje monotonicznie. Jeżeli więc na doświadczalnej krzywej widoczne są periodyczne zmiany nachyleń, to na podstawie ich liczby można ocenić rozrzut rozmiarów ziaren proszku. Na rys. 3.14b widać też, że najszerszym () towarzyszy zmniejszone nachylenie krzywej niskokątowej (czarno-białe prążki przechodzą na dole rysunku w jednolicie szary kolor odpowiadający nachyleniu ). Istotnie, prawo Porod’a jest spełnione w przypadku rozkładu wykładniczo-potęgowego tylko dla dużych wartości , czyli wąskich rozkładów, rys. 3.15.
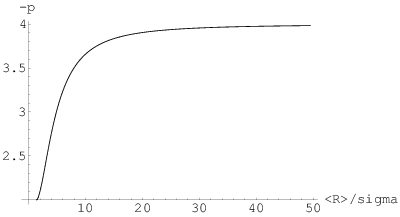
Proszki posiadające szerokie rozkłady mogą więc rozpraszać nawet jak .
Warto wspomnieć jeszcze o alternatywnej interpretacji nachylenia wysokokątowego odcinka krzywej , wiążącej to nachylenie z wymiarem fraktalnym powierzchni rozpraszających drobin: [1]. Nierówność powierzchni drobin jest w gruncie rzeczy substytutem rozkładu ich wielkości. Innymi słowy, można mówić albo o chropowatości powierzchni drobin o identycznych rozmiarach albo, równoważnie, o rozrzucie rozmiarów drobin o idealnie gładkich powierzchniach. Wybór interpretacji zależy od natury materiału rozpraszającego. W przypadku nanokryształu trudno oczekiwać chropowatości powierzchni, skoro jego ścianę powierzchniową buduje niewiele atomów, zaś kryształy mają z natury powierzchnie atomowo gładkie. Nie ma sprzeczności między obiema interpretacjami.
3.5.8 Granice stosowalności metody Scherrera
W §3.4.2 aby wyprowadzić równanie Scherrera porównywaliśmy wyrażenie na profil linii dyfrakcyjnej z połową jego wysokości. Teraz postąpimy podobnie, z tym, że chwilowo zamiast stałej przed wysokością profilu postawimy współczynnik , któremu dopiero później przypiszemy wartość . O proszku zakładamy, że jego rozkład wielkości ziaren jest postaci (3.44). Dla uproszczenia równań posługiwać się będziemy profilem linii (3.5.4) w zmiennych i , przechodząc na samym końcu do zmiennych i .
Porównując wyrażenie na profil linii dyfrakcyjnej proszku o niezerowej dyspersji rozkładu wielkości ziaren (3.5.4) z ułamkiem wysokości tej linii (3.31) otrzymujemy:
| (3.96) |
zaś rozwijając lewą stronę:
| (3.97) | |||||
Po przeniesieniu prawej strony równania ze zmienionym znakiem na lewą, sprowadzeniu do wspólnego mianownika i przegrupowaniu wyrazów dostajemy:
| (3.98) | |||||
Korzystając z faktu, że symbole oraz w powyższym równaniu zawsze występują parami, podstawimy otrzymując:
| (3.99) | |||||
Po zaniedbaniu mianownika i pierwszego członu , który zawsze jest różny od zera mamy:
| (3.100) | |||||
Powyższe równanie jest równaniem przestępnym z dwoma niewiadomymi ( traktujemy jako znane), którego rozwiązaniem jest krzywa . Równanie to można rozwiązać numerycznie traktując zmienne i jako parametry. Ciąg rozwiązań ze względu na parametr , przy ustalonym tworzy monotoniczną krzywą , pokazaną na rys. 3.16 w postaci punktów. Postaci analitycznej tej krzywej niestety nie znamy. Można jednak wykreślić ją dla szerokiego zakresu wartości , który całkowicie pokrywa interesujący przedział zmienności tego parametru. Do tak wykreślonej krzywej można następnie dopasować arbitralnie wybraną funkcję elementarną i traktować ją dalej jako przybliżenie nieznanej analitycznie funkcji . Linia ciągła na rys. 3.16 to dopasowanie funkcji do ciągu rozwiązań równania (3.100):
| (3.101) |
Z rys. 3.16 widać, że jakość dopasowania jest bardzo dobra w całym interesującym nas zakresie wartości parametru i funkcję można traktować dalej jako znaną.
Pamiętając, że poprzednio podstawiliśmy i dysponując zależnością można napisać:
| (3.102) |
co nie jest jeszcze równaniem Scherrera, gdyż w mianowniku zamiast średniego rozmiaru ziarna jest wielkość . Aby otrzymać równanie Scherrera należy pomnożyć (3.102) obustronnie przez , gdyż dopiero jest szerokością połówkową profilu linii:
| (3.103) |
gdzie:
| (3.104) |
Wyrażenie (3.103) ma postać równania Scherrera, ale z (3.104), (3.49) oraz (3.50) wynika, że stała Scherrera wynosi:
| (3.105) |
czyli, że stała Scherrera dla proszków z niezerową dyspersją rozkładu wielkości ziaren (3.44) jest funkcją parametrów tego rozkładu, a więc nie jest to, par excellence, stała. Dla omawianego rozkładu wielkości ziaren zależność ma następującą postać:
| (3.106) |
zaś pełne wyrażenie na szerokość połówkową linii dyfrakcyjnej jest (po podstawieniu ):
Pamiętając, że odwrotność względnej szerokości rozkładu wielkości ziaren (czyli “monodyspersyjność”) to:
| (3.108) |
można przedstawić wartości w zależności od tego parametru, czyli funkcję , co pokazano na rys. 3.17.
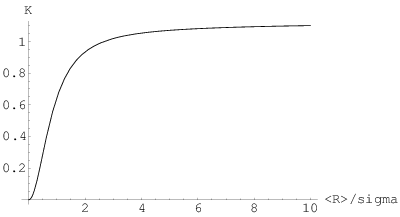
Praktyczną minimalną wartość stałej można ocenić na ok. , ponieważ odpowiada to , czyli dyspersjom większym od . W tej sytuacji ziarna wszystkich rozmiarów występują w porównywalnych ilościach: mamy mieszaninę substancji amorficznej (rozmiar bliski - pojedyncze molekuły) oraz ziaren o innych wielkościach występujących w porównywalnych proporcjach. Wartość maksymalna odpowiada proszkowi składającemu się z ziaren o identycznych rozmiarach, czyli monodyspersyjnemu.
Sens zależności przedstawionej na rys. 3.17 można wyrazić następująco: wartość stałej Scherrera zależy od względnej szerokości rozkładu wielkości ziaren. Co więcej, w realnie obserwowanych przypadkach zależność ta jest bardzo silna. Na przykład nanokrystaliczne proszki świeżo po syntezie (nie poddane żadnej segregacji) mają stosunek w zakresie , co wypada w przedziale silnej zmienności stałej1919 19 Jakkolwiek dziwnie by to nie zabrzmiało. Scherrera. Stosunek ten jest dla materiałów tego samego pochodzenia zawsze podobny (por. §5.3), niezależnie od wielkości zsyntetyzowanych krystalitów. Zmienia go dopiero intencjonalna segregacja (frakcjonowanie). Wyobraźmy sobie, że zsyntetyzowaliśmy krystaliczny proszek posiadający pewien rozrzut wielkości ziarna. Przy pomocy układu sit rozdzielamy go na frakcje o coraz precyzyjniej określonych rozmiarach ziaren. Jednocześnie przy pomocy dyfrakcji proszkowej i równania Scherrera staramy się określać średni rozmiar ziarna w kolejnych frakcjach. Okazuje się niestety, że dla każdej frakcji powinniśmy brać inne stałe Scherrera: mniejsze na początku rozdzielania, kiedy proszek jest jeszcze mieszaniną ziaren różnych wielkości (od, powiedzmy, ) a większe dla frakcji prawie monodyspersyjnych (do ), gdyż zależy właśnie od szerokości rozkładu wielkości ziaren.
Pod znakiem zapytania stoją próby dokładnego oznaczania wielkości ziaren tą metodą w ogóle, skoro do precyzyjnego wyznaczenia wielkości ziarna potrzeba dokładnie znać wartość , a ta zmienia się w funkcji szerokości rozkładu wielkości ziaren, którego właśnie szukamy2020 20 Średni rozmiar ziarna jest jednym z parametrów rozkładu wielkości ziaren.. Ponieważ może zmieniać się w szerokich granicach, od ok. aż do , a więc nawet dwa razy, taki też jest możliwy błąd oznaczenia średniego rozmiaru krystalitów tą metodą.
Trzeba jednak powiedzieć, że dopóki nie przeszkadza nam błąd pomiaru średniej wielkości ziarna na poziomie, przeciętnie, kilkudziesięciu procent, metoda Scherrera jest chyba najprostszą i niezwykle elegancką. Z przedstawionych przykładów wynika jednak, że w zastosowaniach bardziej wymagających potrzebne są raczej metody znalezienia rozrzutu wielkości ziaren.
3.5.9 Granice stosowalności metody Warren’a-Averbach’a
W badaniach mikrostruktury proszków krystalicznych standardem oznaczania rozmiaru i rozkładu wielkości krystalitów2121 21 Metoda Warren’a-Averbach’a umożliwia również badanie naprężeń sieci krystalicznej na podstawie asymetrii linii dyfrakcyjnej. Część naprężeniowa tej teorii nie będzie tutaj dyskutowana. jest metoda Warren’a-Averbach’a (W-A). W oparciu o twierdzenie mówiące, że profil linii dyfrakcyjnej jest transformatą furierowską dystrybucji kształtu krystalitu, można powiedzieć, że metoda W-A jest w istocie analizą dystrybucji kształtu kryształu. W niniejszym paragrafie przedyskutowano wielkości otrzymywane metodą W-A dla proszków polidyspersyjnych w świetle informacji podanych wcześniej.
Dyskusję metody Warren’a-Averbach’a rozpoczniemy od krótkiego przypomnienia jej istoty.
3.5.9.1 Oryginalna teoria
W 1950 roku Warren i Averbach przedstawili metodę wyznaczania średniego rozmiaru krystalitów oraz rozkładu ich wielkości na podstawie kształtu maksimów dyfrakcyjnych [54]. Istota tej metody jest następująca: wybrane maksimum dyfrakcyjne typu , po niezbędnych korektach (odjęcie tła, korekty na poszerzenie instrumentalne, itp.) rozwija się w szereg cosinusów w zakresie obejmującym oba jego ramiona do miejsc, gdzie natężenie znika, rys. 3.18. Początek układu współrzędnych oraz wierzchołek maksimum umieszcza się w środku tego zakresu (rys. 3.18b). Współczynniki rozwinięcia dane są przez:
| (3.109) |
gdzie jest ciągiem punktów pomiarowych tworzących badany refleks w funkcji wektora rozpraszania ( jest natężeniem w maksimum linii, rys. 3.18b); jest całkowitą szerokością analizowanego refleksu; określa odległość w przestrzeni prostej odpowiadającą współczynnikowi . Otrzymane z rozwinięcia (3.109) wartości współczynników układają się na szybko malejącej krzywej (rys. 3.18c). Według [23] jej początkowe nachylenie ekstrapolowane aż do przecięcia z osią wyznacza średnią długość kolumn złożonych z komórek elementarnych kryształu ułożonych jedna za drugą (rys. 3.19a) w kierunku . Średnia jest średnią ważoną, której waga jest równa objętości kolumny, gdyż natężenie promieniowania jest proporcjonalne do objętości materiału rozpraszającego. Wielkość opisuje długość kolumny komórek elementarnych (a nie liczbę komórek elementarnych) i jest liczona w Å.
a)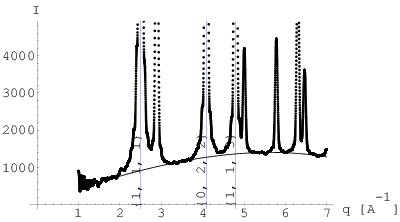
b) 
|
c) 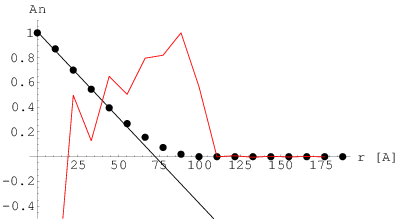
|
a)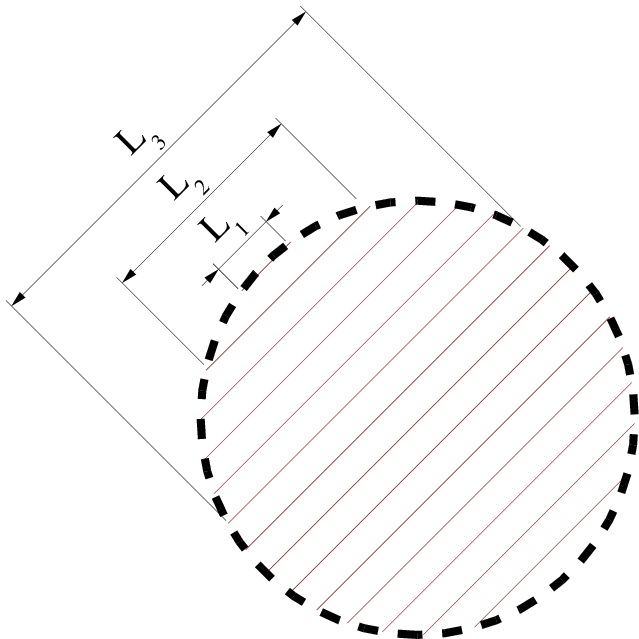 b)
b)
Druga pochodna krzywej tworzonej przez współczynniki rozwinięcia jest rozkładem długości kolumn komórek elementarnych (, Column Length Distribution), również z wagą proporcjonalną do objętości każdej kolumny:
| (3.110) |
Rozkład wyraża więc ułamek objętości kryształu przypadający na kolumny o różnych długościach, a nie liczbę kolumn (rys. 3.19b). Według [55, str.273-275] metodę Warren’a-Averbach’a stosowaną początkowo do refleksów z grupy można używać dla dowolnego refleksu dyfraktogramu proszkowego. Zarówno rozkład długości kolumn komórek elementarnych jak i jego wartość średnia odnosi się zawsze do konkretnego kierunku krystalograficznego, zdefiniowanego przez indeks refleksu , którego dotyczy analiza. Profil (szerokość) linii odnosi się więc do rozmiaru (szerokości) kryształu w kierunku w przestrzeni prostej. “Kierunkowość” metody W-A powoduje, że zastosowana do różnych refleksów kryształów o silnej anizotropii kształtu daje różne wyniki dla każdego z kierunków.
Na rys. 3.18 przedstawiono przykład analizy Warren’a-Averbach’a przeprowadzonej na podstawie dyfraktogramu “idealnego” ziarna w kształcie kuli o średnicy Å, bez dyspersji rozmiaru, obliczonego numerycznie (ab initio), nie zawierającego z definicji poszerzeń, przesunięć lub asymetrii pochodzących od układu eksperymentalnego. Z porównania kształtu rozkładu długości kolumn z rys. 3.19b i takiego samego rozkładu otrzymanego metodą W-A z analizy dyfraktogramu obliczonego ab initio (rys. 3.18c, czerwona łamana linia) widać, że mają one zbliżony charakter. Wyliczona z analizy W-A średnia długość kolumny w krystalicie dla testowego dyfraktogramu (rys. 3.18) wynosi Å. Nie jest to rozmiar ziarna ale średnia długość kolumny komórek elementarnych. Zazwyczaj interesujący jest jednak właśnie rozmiar, lecz aby go na podstawie obliczyć trzeba znać kształt ziarna. Kształt krystalitu najczęściej nie jest z góry znany i często przyjmuje się, że jest kulisty. W takim wypadku średnia długość kolumny odpowiada wysokości walca o objętości równej objętości naszego ziarna i podstawie równej wielkiemu kołu naszego ziarna. Trzymając się oznaczeń, w których jest rozmiarem, a więc tutaj średnicą (nie promieniem!) ziarna piszemy:
| (3.111) |
skąd rozmiar ziarna:
| (3.112) |
Tak więc otrzymaną z analizy W-A średnią długość kolumny należy pomnożyć przez aby uzyskać rozmiar ziarna. W tym testowym przypadku Å.
Pomimo że analizowane dane pochodziły z obliczeń numerycznych wykonanych dla proszku bez dyspersji rozmiarów, były wolne od szumu i próbkowane z krokiem Å, wynik obarczony jest błędem. Powstaje pytanie, czy rozmiar krystalitu obliczany ze średniej długości kolumn jest rozmiarem średnim ziarna w proszku? Zanim odpowiemy na to pytanie, spróbujemy zinterpretować sens analizy W-A w świetle informacji zawartych w rozdziale 3.
3.5.9.2 Interpretacja otrzymywanych wielkości
Wiedząc z rozdziału 3, że profil proszkowej linii dyfrakcyjnej jest transformatą furierowską dystrybucji kształtu rozpraszającego kryształu łatwo zauważyć, że analiza danych dyfrakcyjnych metodą Warren’a-Averbach’a, polegająca na wykonaniu cosinusowej transformaty Fouriera przeprowadza analizowaną linię dyfrakcyjną z powrotem w dystrybucję kształtu ziarna (por. kropkowaną linię rozwinięcia w szereg cosinusów z rys. 3.18c i 3.9d). Korzystając z metody W-A wyznacza się najpierw pochodną dystrybucji kształtu w punkcie , będącą współczynnikiem kierunkowym prostej używanej potem do ekstrapolacji rozmiaru ziarna. Rozwiązanie równania tej prostej wyznacza miejsce jej przecięcia z osią (rys. 3.18c) i, według [23], średnią długość kolumny komórek elementarnych w krysztale.
Należy podkreślić, że średnia długość kolumny komórek elementarnych otrzymywana z doświadczalnych danych dyfrakcyjnych metodą W-A jest uśredniona podwójnie. Raz, bo w każdym krysztale mamy zbiór kolumn różnych długości; dwa, bo mamy w proszku mieszaninę kryształów o różnych rozmiarach. Jeśli porównać kryształy do ziemniaków a kolumny do frytek, to średnia długość frytek otrzymanych z jednego ziemniaka jest pierwszym stopniem uśrednienia, a średnia frytka zrobiona z wielu ziemniaków o różnych wielkościach - drugim.
Prześledzimy wyniki procedury W-A zastosowanej do kilku typów proszków, wyprowadzając relacje pomiędzy długością kolumny (frytki) a rozmiarem ziarna (ziemniaka) dla kilku rodzajów proszków. Najpierw zajmiemy się proszkiem bez rozrzutu rozmiarów ziaren, potem przejdziemy do bardziej realnych układów z niezerową dyspersją rozkładu wielkości ziaren.
Rozmiar ziarna w proszku monodyspersyjnym
Przyjmując, że mamy do czynienia z kryształami objętościowymi (por. §3.4.2), można użyć jawnej postaci dystrybucji kształtu kuli danej wzorem (3.35) i zapisać współczynnik kierunkowy prostej ekstrapolującej średnią długość kolumn w metodzie Warren’a-Averbach’a jako:
| (3.113) |
gdzie jest rzeczywistym, poszukiwanym rozmiarem ziarna. W tej sytuacji równanie prostej ekstrapolującej jest postaci:
| (3.114) |
gdyż dystrybucja kształtu w wynosi . Miejsce zerowe prostej, czyli średnia długość kolumny otrzymywana z metody W-A wynosi:
| (3.115) |
Otrzymaliśmy więc wynik identyczny jak w oryginalnej teorii. W celu obliczenia średniej długości kolumny dla bardziej realnych układów - proszków z rozrzutem wielkości ziaren - wymagane jest uśrednienie dystrybucji kształtu ziarna po rozmiarach wszystkich ziaren obecnych w proszku.
Rozmiar ziarna w proszku polidyspersyjnym
Poprzednio pokazaliśmy, że dla proszku monodyspersyjnego istnieje liniowa relacja pomiędzy rozmiarem ziarna a długością kolumny komórek elementarnych wyznaczaną metodą Warren’a-Averbach’a, co stanowi podstawę jej działania. Sprawdzimy teraz postać tej samej relacji dla proszków złożonych z kulistych ziaren z rozrzutem rozmiarów. Procedury Warren’a-Averbach’a użyjemy w odniesieniu do dystrybucji kształtu uśrednionej po rozmiarach wszystkich krystalitów w proszku :
| (3.116) | |||||
Pochodna dystrybucji kształtu w zerze ma postać , gdzie jest stałą zależną od kształtu ziarna, np. dla kryształów kulistych czy dla kryształów w formie graniastosłupa. Stąd:
| (3.117) |
Tak więc średnia długość kolumny komórek elementarnych otrzymywana z analizy W-A jest proporcjonalna do odwrotności momentu statystycznego rzędu rozkładu wielkości ziaren . Przeciwnie do momentu rzędu , który jest wartością średnią rozkładu (czyli średnim rozmiarem ziarna), moment nie jest stowarzyszony z żadną fizycznie interpretowalną wielkością. Założenie teorii W-A o liniowej relacji pomiędzy średnią długością kolumny a średnim rozmiarem ziarna jest więc spełnione tylko w szczególnych przypadkach, np. o ile zachowana jest równość:
| (3.118) | |||||
| (3.119) |
Jest to prawda, np. gdy:
| (3.120) |
czyli gdy rozkład wielkości ziaren ma postać delty Dirac’a. Wtedy całki po obu stronach równania znikają i otrzymujemy tożsamość . Innymi słowy, w ogólności, metoda Warren’a-Averbach’a działa poprawnie pod warunkiem braku rozrzutu wielkości krystalitów w proszku (). Jednak rzeczywiste proszki zawsze posiadają pewną dyspersję rozmiarów ziaren. Postaramy się określić wpływ dyspersji na możliwe błędy na przykładzie wykładniczo-potęgowego i log-normalnego rozkładu wielkości ziaren.
Średni rozmiar ziarna w proszku o wykładniczo-potęgowym rozkładzie wielkości ziaren
W celu wyprowadzenia relacji pomiędzy średnim rozmiarem ziarna a średnią długością kolumny komórek elementarnych wyznaczaną metodą Warren’a-Averbach’a, scałkujemy dystrybucję kształtu kuli (3.29) z wykładniczo-potęgowym rozkładem wielkości ziaren (3.44) i znajdziemy pochodną tej całki dla bliskich zera. Całka wynosi:
| (3.121) | |||||
gdzie i są parametrami wykładniczo-potęgowego rozkładu wielkości ziaren, zaś jest funkcją gamma Euler’a. Jest to dystrybucja kształtu średniego ziarna proszku dla . Podobnie jak poprzednio obliczymy pochodną tej dystrybucji, stanowiącą współczynnik kierunkowy prostej, używanej w metodzie W-A do ekstrapolacji średniego rozmiaru ziarna:
| (3.122) |
skąd średnia długość kolumny wyznaczanej z analizy W-A jest, po podstawieniu (3.49) i (3.50):
| (3.123) |
Średni rozmiar ziarna wynosi:
| (3.124) |
Wyrażenie pod pierwiastkiem można rozwinąć w szereg względem wokół zera i zaniedbać wyższe wyrazy:
| (3.125) |
Korzystając dla z przybliżenia monodyspersyjnego (3.112) i pamiętając, że współczynnik zmienności rozkładu jest , można powyższe zapisać jako:
| (3.126) |
Procentowy błąd metody stanowi wyraz dodany do jedności pod nawiasem kwadratowym:
| (3.127) |
Jak widać średnia długość kolumny (3.123) dla proszków z rozkładem wielkości ziaren zależy od dyspersji tego rozkładu. Dla dyspersji wyraźnie mniejszych od zależność ta jest słaba z powodu drugiej potęgi przy obu zmiennych. W granicy wyrażenie (3.123) redukuje się do postaci odpowiadającej proszkowi bez dyspersji rozmiarów ziaren (3.115). Oznacza to, że metoda Warren’a-Averbach’a poprawnie funkcjonuje dla proszków z nieznaczną dyspersją rozmiarów, co pokazano na rys. 3.20.
W praktyce doświadczalnej mamy często do czynienia ze znacznymi dyspersjami. Rozrzut wielkości ziaren zawsze obecny w rzeczywistych proszkach może być przyczyną istotnych rozbieżności wyników otrzymywanych metodą W-A i technikami mikroskopowymi. Dla upewnienia się, że wyniki analizy W-A zależą od szerokości rozkładu wielkości ziaren proszku nie tylko dla rozkładu wykładniczo-potęgowego, sprawdzony zostanie jeszcze przypadek najpowszechniej występującego rozkładu log-normalnego.
Średni rozmiar ziarna w proszku o log-normalnym rozkładzie wielkości ziaren
Dystrybucja kształtu odpowiadająca uśrednionemu ziarnu w proszku o log-normalnym rozkładzie wielkości ziaren dla bliskich zera wynosi:
| (3.128) | |||||
gdzie jest medianą zaś dyspersją rozkładu normalnego zmiennej . Pochodna tej dystrybucji, wzięta w zerze i stanowiąca współczynnik kierunkowy dla ekstrapolacji w metodzie Warren’a-Averbach’a jest:
| (3.129) |
zatem średnia długość kolumny (por. (4.6)):
| (3.130) |
zaś średni rozmiar ziarna:
| (3.131) |
Pamiętając, że współczynnik zmienności rozkładu log-normalnego (4.9) jest , można powyższe przepisać jako:
| (3.132) |
skąd procentowy błąd metody wyjmiemy łatwo jako ów dodatek do jedynki pod nawiasem kwadratowym:
| (3.133) |
Podobnie jak w przypadku rozkładu wykładniczo-potęgowego, otrzymywana z metody W-A średnia długość kolumny jest nie tylko funkcją rozmiaru ale też i dyspersji rozmiarów ziaren, której a priori nie znamy. Wyznaczany zaś średni rozmiar ziarna jest nie tylko liniową funkcją średniej długości kolumny (czego oczekiwaliśmy) ale też kwadratową funkcją względnej szerokości rozkładu wielkości ziaren (co jest niepożądane). W praktyce nietrudno spotkać proszki, w których (por. §5.2 oraz rys. 5.14) i błąd oznaczenia osiąga sto procent. Tak więc nie można precyzyjnie podać rozmiaru ziaren bez znajomości dyspersji, a więc bez wyznaczenia pełnego rozkładu ich wielkości (por. [27]).
Rozkład wielkości ziaren w metodzie W-A
W dość powszechnie panującej opinii metoda Warren’a-Averbach’a bezpośrednio wyznacza rozkład wielkości ziaren proszku jako drugą pochodną szeregu cosinusów analizowanej linii dyfrakcyjnej [23, str.652]. Utożsamienie rozkładu długości kolumn komórek elementarnych (który metoda W-A rzeczywiście wyznacza) i rozkładu wielkości ziaren jest jednak nadinterpretacją, która pojawiła się w pracach nawiązujących do oryginalnej książki Warrena [55]. W oryginale autor nie tylko nie mówi o rozkładzie wielkości ziaren, ale dodatkowo wskazuje, że możliwość uzyskania rozkładu długości domen “ma raczej ograniczone znaczenie, ponieważ druga pochodna wielkości mierzonej doświadczalnie, jak , jest obarczona dużym błędem i co więcej, metoda oddzielania czynników związanych z rozmiarem i naprężeniami sieci jest ograniczona do małych wartości ” [55, str.272].
W rzeczywistości przejście od rozkładu długości kolumn komórek elementarnych do rozkładu wielkości ziaren nie jest proste [24]. Druga pochodna szeregu , czyli dystrybucji kształtu, (wzięta z minusem) nie może być interpretowana bezpośrednio jako rozkład wielkości ziaren z wyjątkiem jednego szczególnego przypadku: wybranych refleksów ziaren o bardzo specyficznych kształtach (por. §3.4.1). Dystrybucja kształtu ziaren charakteryzujących się stałością przekroju poprzecznego na całej swojej długości, czyli posiadających formę graniastosłupa (rys. 3.8) ma postać linii prostej załamanej w miejscu odpowiadającym długości ziarna (rys. 3.9a). Druga pochodna takiej linii daje ostre maksimum w miejscu wyznaczającym rozmiar ziarna, zaś w przypadku mieszaniny krystalicznych prostopadłościanów o różnych długościach dostaniemy rozkład wielkości ziaren. Dotyczyć to będzie jednak tylko rodziny maksimów dyfrakcyjnych o indeksach odpowiadających kierunkowi, w którym kryształ ma stały przekrój. W praktyce sytuację taką spotyka się w nielicznych materiałach o strukturze regularnej, np. .
3.6 Błędy pomiarowe
Oznaczenie stałej sieci polega na ustaleniu pozycji pików jakąś metodą, najczęściej fitowania jednej lub więcej linii jednocześnie. Fitowanie nie musi być jednoznaczne, a jego wynik jest estymatą mierzonej wartości. Estymatą o błędzie, na który wpływ ma wiele czynników, w tym szum. Spróbujemy tu podać oszacowanie błędu stałej sieci i rozmiaru ziarna spowodowanego szumem. Oszacowanie nie uwzględnia innych źródeł błędów, np. systematycznych błędów metod pomiarowych (por. §3.5.8, §3.5.9).
Założenie: dopasowanie profilu linii (albo pomiar jej szerokości) jest dobre, to znaczy dopasowany profil mieści się w zakresie szumu pomiarowego krzywej doświadczalnej (blisko chwilowej wartości średniej sygnału, nigdy nie wychodzi poza amplitudę szumu) w całym zakresie analizowanego piku.
3.6.1 Oszacowanie błędów pomiarowych stałej sieci
Weźmy dystrybucję kształtu kuli daną przez (3.29) oraz jej transformatę furierowską, czyli profil linii dyfrakcyjnej dany przez (3.35) i unormujmy profil do jedności w jego maksimum (nie chodzi o natężenie integralne) dzieląc go przez (3.36):
gdzie jest natężeniem zmierzonego profilu w jego maksimum (nie chodzi o natężenie integralne). Znajdźmy drugą pochodną profilu linii, żeby potem ustalić jego punkty przegięcia:
Za chwilę będziemy ją przyrównywać do zera, więc zaniedbajmy mianownik (i tak nie może się zerować), a także stałe przed nawiasem kwadratowym:
Traktując jako pojedynczą zmienną, numerycznie łatwo ustalić, że miejsce zerowe drugiej pochodnej (punkt przegięcia) profilu wypada dla . Obliczymy natężenie profilu w miejscu przegięcia. W tym celu w wyrażeniu na profil linii podstawiamy :
Amplituda szumu w miejscu przegięcia profilu będzie odpowiednio (z rozkładu Bernoulli’ego):
Chcąc znaleźć nachylenie profilu w najbardziej stromym miejscu, czyli w punkcie przegięcia, musimy obliczyć wartość pochodnej tamże. Najpierw sama pochodna:
Na koniec z podstawieniem mamy:
Niedokładność położenia linii znajdziemy z amplitudy szumu w punkcie przegięcia po podzieleniu go przez tangens kąta nachylenia profilu w tym miejscu, czyli przez pochodną profilu:
| (3.134) |
Niedokładność oznaczenia odległości międzypłaszczyznowych będzie zatem:
| (3.135) |
gdzie jest położeniem linii doświadczalnej w funkcji wektora rozpraszania. Ustalając promieniowanie o długości fali mamy:
| (3.136) |
Czyli im większe ziarno i kąt bragowski , tym mniejszy błąd oznaczenia stałej sieci. Z drugiej strony: w przypadku fotonów rentgenowskich, natężenie kolejnych linii spada z kątem, co powiększa błąd . Te dwie tendencje w przybliżeniu znoszą się. Ustalając jakiś wygodny kąt bragowski, np. (odpowiednie ), błąd można przybliżyć jako:
| (3.137) |
Na rys. 2.17a przedstawiono zależność wielkości błędu stałej sieci od rozmiaru ziarna i statystyki pomiaru analizowanego piku dyfrakcyjnego.
3.6.2 Oszacowanie błędów pomiaru rozmiaru ziarna
Korzystając ze wzoru (3.134):
można oszacować niedokładność oznaczenia rozmiaru ziarna jako:
| (3.138) |
gdzie jest liczbą zliczeń w maksimum analizowanego piku. Czyli: im większa liczba zliczeń (lepsza statystyka) tym mniejszy błąd oznaczenia jego rozmiaru.
Na rys. 2.17b przedstawiono zależność wielkości błędu rozmiaru krystalitów od statystyki pomiaru analizowanego piku dyfrakcyjnego i rozmiaru ziarna.