Chapter 4 Metody numeryczne
Obliczenia numeryczne dyfrakcji są dość podobne do korzystania z teorii analitycznej, ale dają więcej “swobody manewru” tam, gdzie teoria wiąże nas swoimi założeniami (np. że ziarna mają być kuliste). Z wad: są bardziej pracochłonne i wymagają użycia pojęć, które w czasie wyprowadzania teorii co prawda gdzieś się pojawiły, ale zaraz potem znikły wycałkowane w niebyt. W obliczeniach numerycznych, niestety, musimy tych pośrednich pojęć używać bezpośrednio i to ilościowo (komputery nie lubią “stałych proporcjonalnych do…” albo “małych drugiego rzędu”). Musi być konkretnie, dlatego pobieżnie wzmiankowane w poprzednich rozdziałach pojęcia muszą być opisane tutaj z bolesnymi szczegółami. W pierwszej części (§4.1) podano więcej informacji na temat:
-
•
funkcji rozkładu radialnego ,
-
•
funkcji korelacji par i
-
•
dystrybucji kształtu .
Dwie pierwsze funkcje opisują statystykę odległości międzyatomowych i są nierzadko utożsamiane. Najszerzej stosowana oznacza średnią gęstość elektronową wokół wybranego punktu i jest zależna od struktury materiału (tzn. jest różna dla różnych struktur krystalicznych, ciał amorficznych i rozcieńczonych gazów). Opisuje ona struktury nieograniczone przestrzennie (np. kryształ idealny). Funkcja korelacji par jest ograniczoną przestrzennie odmianą . Odnosi się ona do fizycznego obiektu (np. krystalitu) a nie do jego struktury i znika dla odległości większych od rozmiaru tego obiektu. Obie wielkości łączy dystrybucja kształtu obiektu , będąca w obliczeniach kluczowym pojęciem i stanowiąca matematyczny opis mikrostruktury nanokryształów mierzonej dyfrakcyjnie. W szczególnym przypadku obiektów o rozmiarach makroskopowych, np. dużych krystalitów, dystrybucja kształtu jest w przybliżeniu stała i równa jedności, co uzasadnia utożsamianie i : kryształ uznajemy wtedy za nieskończony, a pojęcia “kryształ” i “struktura krystaliczna” stają się synonimami.
W pierwszej części niniejszego rozdziału wprowadzono także pojęcia funkcji korelacji warstw i rozkładu wielkości ziaren pozwalające na uwzględnienie wpływu jednowymiarowego nieuporządkowania i rozrzutu wielkości krystalitów w obliczanych ab initio dyfraktogramach proszkowych.
W paragrafie 4.2, przy okazji prezentowania podstaw obliczeń ab initio dyfraktogramów proszkowych, dokonano przekształceń wzoru Debye’a. Pokazano, że jest on równoważny furierowskiej transformacie funkcji korelacji par krystalitu. Następnie został zapisany w postaci transformaty iloczynu funkcji i . Dzięki takiemu przekształceniu można przyspieszyć obliczenia ab initio o kilka rzędów wielkości.
4.1 Definicje
4.1.1 Funkcja rozkładu radialnego, RDF
Funkcja rozkładu radialnego (Radial Distribution Function, ) jest zdefiniowana następująco: jest to prawdopodobieństwo znalezienia atomu w odległości z przedziału od dowolnego atomu odniesienia (wybranego za początek układu współrzędnych):
| (4.1) |
gdzie jest liczbą atomów w jednostce objętości w odległości (od dowolnie wybranego atomu odniesienia). Funkcję rozkładu radialnego przedstawiono na rys. 4.1.
Fizyczne znaczenie polega na opisie średniego otoczenia dowolnego atomu w rozważanej strukturze (np. krystalicznej).
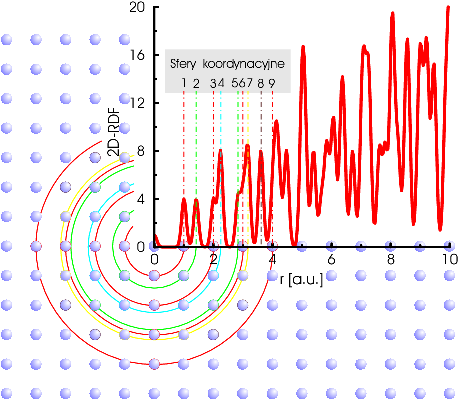
Funkcja rozkładu radialnego odnoszona do atomów rozumianych jako punkty w przestrzeni jest dyskretna. Jej nieskończenie wąskie maksima odpowiadają kolejnym odległościom międzyatomowym. W praktyce ruchy termiczne atomów powodują, że szerokość maksimów jest skończona (rys. 4.1). Postać zależy też od stopnia uporządkowania struktury: jest różna w kryształach, ciałach amorficznych i cieczach.
4.1.1.1 RDF kryształów
Periodyczny przestrzenny rozkład atomów w krysztale powoduje “gromadzenie się” atomów na stosunkowo nielicznych sferach, nazywanych sferami koordynacyjnymi (rys. 4.1). Sfery koordynacyjne stanowią kolejne warstwy atomów odległych o identyczny dystans od wybranego centrum. Dla kryształów ma postać szeregu bardzo ostrych maksimów wypadających w odległościach właściwych dla kolejnych sfer koordynacyjnych i numerujących te sfery (rys. 4.1).
Dzięki istnieniu w krysztale uporządkowania dalekiego zasięgu wyraźne maksima mierzonych doświadczalnie funkcji są widoczne dla stosunkowo dużych (w praktyce widać nawet pierwszych kilkanaście maksimów). Zagęszczenie dalszych sfer koordynacyjnych w połączeniu z niską rozdzielczością danych dyfrakcyjnych11 1 Z własności transformaty Fouriera wynika konieczność posiadania danych dyfrakcyjnych w szerokim zakresie wektora rozpraszania dla uzyskania o wysokiej rozdzielczości . Z racji silnego zanikania czynnika atomowego w funkcji kąta, użycie promieni X do otrzymania dyfraktogramów o jest bardzo trudne, zaś praktycznie niemożliwe. powoduje, że dla bardzo dużych (rzędu kilkudziesięciu sfer koordynacyjnych) odległość sąsiednich maksimów staje się mniejsza niż ich szerokość połówkowa i maksima te zlewają się. Ogranicza to użyteczność mierzonych doświadczalnie funkcji do opisu najbliższego otoczenia atomu.
Funkcja rozkładu radialnego w strukturach krystalicznych o symetrii trójwymiarowej (czyli w takich, w których istnieje komórka elementarna22 2 Co jest spełnione dla większości “normalnych” kryształów. Kryształy politypowe mają komórki elementarne rozciągłe w kierunku i często bardzo duże. W kryształach z błędami ułożenia nie ma komórki elementarnej.) można rozłożyć na składowe, z których każda odpowiada otoczeniu jednego atomu komórki elementarnej; otoczenia te są w ogólności różne i po uśrednieniu tworzą całej struktury:
| (4.2) |
gdzie indeks przebiega wszystkie atomy komórki elementarnej.
4.1.1.2 RDF ciał amorficznych i cieczy
W ciałach amorficznych i cieczach nie ma uporządkowania dalekiego zasięgu - jedynie atomy pierwszych dwóch, trzech sąsiadów znajdują się w odległościach skorelowanych wystarczająco do wytworzenia maksimów funkcji . Liczba wyraźnych maksimów stanowi często używane kryterium amorficzności (rys. 2.1) i jest stosowana jako miara uporządkowania ciał przy opisie wstępnych stadiów krystalizacji.
W fizyce nanomateriałów można stosować m.in. do badania stanu powierzchni nanokryształów [33]. Znając postać dla nieskończonej struktury, można mierzyć odchylenia położeń pierwszych sfer koordynacyjnych nanokryształu od wartości “idealnych”, wnioskując tym samym o naprężeniach lub zrelaksowaniu sieci na granicy ziaren.
4.1.1.3 RDF a rozmiar kryształu
Postać funkcji rozkładu radialnego z definicji nie zależy od wyboru początku układu współrzędnych, gdyż opisuje strukturę nieskończenie rozciągłą, np. nieograniczoną sieć krystaliczną. W praktyce posługujemy się nią w odniesieniu do ciał, których wymiary geometryczne są skończone, ale dużo większe niż zakres odległości , który chcielibyśmy analizować (zazwyczaj kilkadziesiąt Å). Dla ciał o skończonych rozmiarach statystyka odległości międzyatomowych zależy od wyboru węzła początkowego - jest inna dla węzła znajdującego się w pobliżu powierzchni ciała, a inna dla węzła w jego wnętrzu. O ile prawdopodobieństwo znalezienia atomu przypowierzchniowego w krysztale mikrometrowym lub większym jest nieznaczne i możemy je zaniedbać, o tyle dla nanokryształów jest bliskie 1.
Inaczej mówiąc, statystyka odległości międzyatomowych nieskończonego kryształu (czyli ) i taka sama statystyka izolowanego nanokryształu w próżni to inne funkcje, podobne w zakresie małych ale zupełnie różne dla dużych.
W dalszym ciągu będziemy traktować funkcję jako właściwość struktury ciała a nie jej konkretnej realizacji, np. w postaci nanokryształu. Pomimo, że w literaturze spoza dziedziny nanotechnologii te dwa pojęcia bywają utożsamiane, pod pojęciem rozumieć będziemy funkcję rozkładu radialnego struktury nieskończenie rozciągłej. Dla układów o skończonych rozmiarach, np. izolowanych kryształów nanometrowych, jako odpowiednika będziemy używać funkcji korelacji par (Pair Correlation Function, ).
4.1.2 Funkcja korelacji par, PCF
Funkcja korelacji par (Pair Correlation Function, ) nazywana jest również Funkcją dystrybucji par (Pair Distribution Function, ) lub Funkcją odległości międzyatomowych (Interatomic Distance, ).
Funkcja korelacji par jest gęstością prawdopodobieństwa, że dwa atomy oraz odległe od siebie o należą do tego samego krystalitu. W praktyce jest to histogram odległości pomiędzy wszystkimi parami atomów w krystalicie [59]. W tej ostatniej sytuacji funkcja korelacji par jest unormowana nie do jedności lecz do całkowitej liczby par atomów w drobinie ( gdzie jest liczbą atomów w drobinie).
Zależnie od tego, czy traktujemy materię jako ciągłą albo ziarnistą, przybiera postać, odpowiednio, ciągłą bądź dyskretną.
-
1.
Dyskretna funkcja korelacji par (patrz rys. 4.2a) jest statystyką odległości pomiędzy atomami pojedynczego krystalitu. Dysponując funkcją korelacji par atomów krystalitu, można obliczyć dyfraktogram proszku składającego się z takich, przypadkowo zorientowanych, krystalitów. Właśnie dyskretna postać funkcji , w zakresie małych (odzwierciedlająca istnienie uporządkowania bliskiego zasięgu) i dużych (uporządkowanie dalekiego zasięgu33 3 Warunkiem dyskretnej postaci dla dużych jest periodyczność sieci. ), pociąga za sobą powstawanie maksimów interferencyjnych (tzw. refleksów bragowskich).
a)
 b)
b)
Figure 4.2: a) Dyskretna Funkcja korelacji par dla krystalitu w kształcie kuli o średnicy Å (unormowana do całkowitej liczby par atomowych krystalitu), b) ciągła Funkcja korelacji par dla kuli o średnicy Å (unormowana do jedności). -
2.
Ciągła funkcja korelacji par (patrz rys. 4.2b) jest statystyką odległości pomiędzy wszystkimi elementami objętości należącymi do pojedynczego kawałka ciągłej materii. Znając tę funkcję np. dla aglomeratu zbudowanego z układu kilku-kilkudziesięciu ziaren można wyliczyć profil rozpraszania niskokątowego takiego układu. Rozpraszanie niskokątowe () odzwierciedla strukturę obiektów o wymiarach Å czyli znacznie większych niż odległości międzyatomowe. Ciągła postać funkcji jest związana z postrzeganiem takich obiektów jako ciągłej materii o ustalonej gęstości z zaniedbaniem szczegółów jej struktury atomowej. Obliczone profile rozpraszania niskokątowego proszków mają postać gładkich funkcji, najczęściej bez wyraźnych maksimów interferencyjnych.
4.1.2.1 PCF vs. RDF
Jak powiedziano, w badaniach niezwiązanych z nanotechnologią funkcje korelacji par i rozkładu radialnego są utożsamiane. Utożsamienie to jest czynione na podstawie (często niejawnego) założenia, iż ma się do czynienia z układem jednorodnym, (praktycznie) nieograniczonym w przestrzeni (np. dużym kryształem, ośrodkiem ciągłym). Jednak dla układów ograniczonych przestrzennie, jakimi niewątpliwie są kryształy nanometrowe, założenie to nie jest spełnione (patrz zanikanie wobec nieskończonego wzrostu na rys. 4.3 ).
W układach ograniczonych przestrzennie funkcje oraz związane są zależnością, rys. 4.3:
| (4.3) |
gdzie jest to dystrybucja kształtu krystalitu o rozmiarze . Funkcję tę omówimy dokładnie w następnym paragrafie.
4.1.3 Dystrybucja kształtu, SD
Dystrybucja kształtu (Shape Distribution, ) jest statystycznym opisem kształtu trójwymiarowej bryły. Opisuje ona kształt poprzez podanie rozkładu prawdopodobieństwa parametru, będącego funkcją współrzędnych losowo wybranych punktów należących do tej bryły [32], np.
-
•
odległości pomiędzy dwoma losowo wybranymi punktami w objętości kuli,
-
•
kąta utworzonego przez trzy losowo wybrane punkty na powierzchni walca,
-
•
odległości pomiędzy środkiem kuli a losowo wybranym punktem na jej powierzchni,
-
•
pierwiastka kwadratowego z powierzchni trójkąta rozpiętego nad trzema losowy wybranymi punktami sfery, itp.
Dystrybucje kształtu mierzące prawdopodobieństwa odległości pomiędzy dwoma losowymi punktami powierzchni kilku prostych figur przedstawione są na rys. 4.4.
4.1.3.1 Dystrybucja kształtu a PCF
Zasadnicze znaczenie dla obliczeń dyfrakcji proszkowej ma znajomość
funkcji korelacji par . Funkcję tę możemy przedstawić jako
iloczyn dystrybucji kształtu i funkcji rozkładu radialnego (4.3).
Przyczyna, dla której dokonujemy rozdzielenia funkcji korelacji par
na te dwie składowe leży w definicji
prawdopodobieństwa warunkowego:
gęstość prawdopodobieństwa tego, że para punktów odległa o należy do ziarna
=
prawdopodobieństwo warunkowe, że para punktów należy do ziarna o rozmiarze
pod warunkiem, że odległość między nimi wynosi
x
gęstość prawdopodobieństwa, że odległość dwóch punktów jest .
UWAGA: ostatni człon jest gęstością prawdopodobieństwa bezwarunkowego, a zatem dotyczy nieograniczonego kryształu, czyli odpowiada struktury.
Dystrybucja kształtu krystalitu zależy oczywiście od kształtu krystalitu, a ten zazwyczaj nie jest dokładnie znany. Szczególnie w przypadku nanokryształów, ustalenie wyglądu ziarna metodami mikroskopowymi może być trudne. Zresztą nawet znajomość kształtu ziarna nie przesądza kształtu krystalitu, gdyż często mamy do czynienia z ziarnami będącymi aglomeratami wielu krystalitów. Z braku szczegółowych informacji o kształcie krystalitu często zakłada się, że jest on izotropowy i przybliża go dystrybucją kształtu kuli. Jej postać jest zresztą jedną z nielicznych dystrybucji kształtu znanych analitycznie. Ona też będzie używana do obliczania funkcji korelacji par i dalej - dyfraktogramów proszkowych.
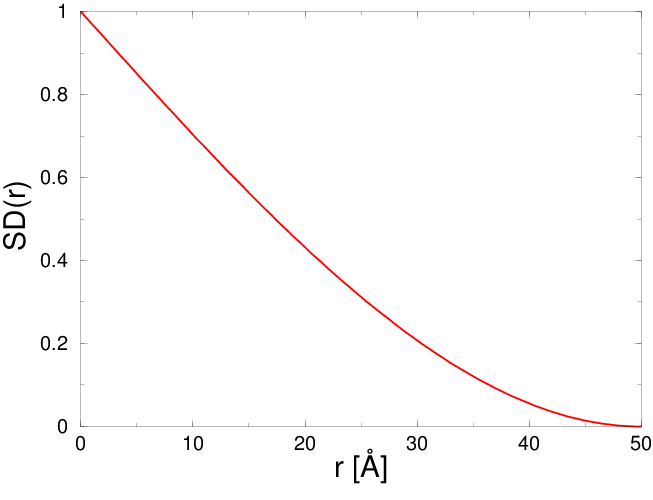
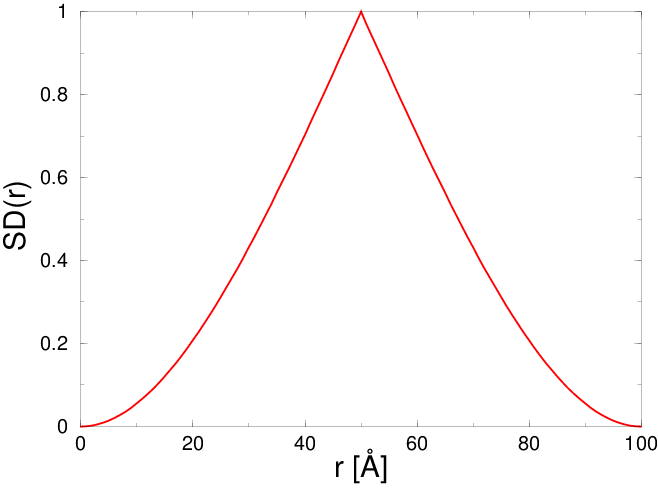
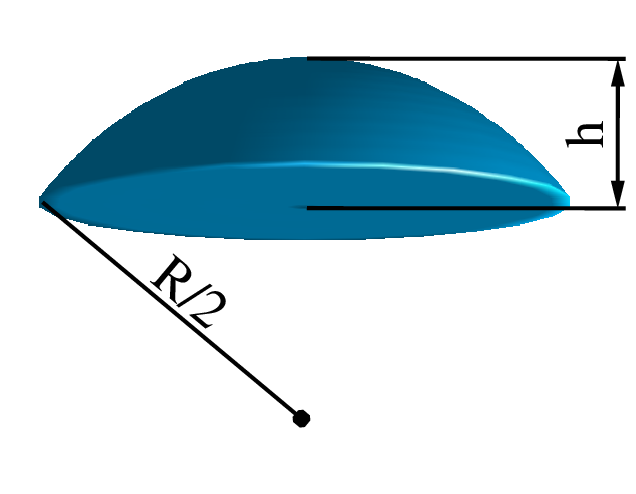
Ze względu na zakres zastosowań można wyróżnić dwie najważniejsze dystrybucje kształtu (patrz rys. 4.5):
| a) |  |
 |
|---|---|---|
| b) |  |
 |
-
1.
Mierzącą prawdopodobieństwo odległości pomiędzy dwoma losowo wybranymi punktami w objętości kuli. Jest ona użyteczna do wyliczania profili dyfrakcyjnych ziarna izolowanego, czyli hipotetycznego proszku sporządzonego z identycznych kulistych ziaren, krystalograficznie zorientowanych względem siebie całkowicie przypadkowo (proszek idealny).
-
2.
Mierzącą prawdopodobieństwo odległości pomiędzy dwoma losowo wybranymi punktami należącymi do dwóch sąsiadujących kul. Jest ona użyteczna do budowania modeli mikrostruktury proszków nanometrowych i symulacji profili rozpraszania niskokątowego ().
W dalszym ciągu pod pojęciem dystrybucja kształtu rozumiana będzie pierwsza z tych dystrybucji.
4.1.3.2 Obliczanie Dystrybucji Kształtu
Wyobraźmy sobie w przestrzeni ziarno (okruch materii) o rozmiarze (średnicy) . Oznaczmy przez dowolny punkt w jego objętości. Następnie umieśćmy w losowym miejscu w przestrzeni drugi punkt . Dystrybucja Kształtu ziarna jest to prawdopodobieństwo , że punkt należy do ziarna, gdzie . Oczywiście, i , rys. 4.6. Ponieważ , więc , czyli jest parzysta (symetryczna względem osi ).
a)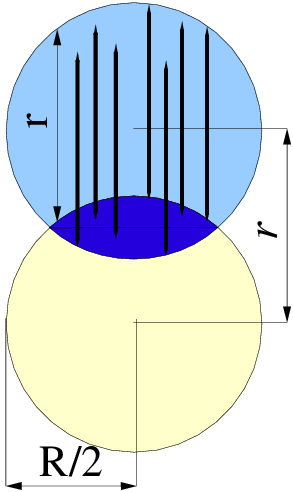
|
b)
|
Dystrybucję kształtu prostych figur geometrycznych można opisać wyrażeniem analitycznym. Dystrybucja kształtu kuli o rozmiarze44 4 Symbol oznacza tutaj ,,rozmiar”. Rozmiarem kuli jest jej średnica. Dlatego oznacza w odniesieniu do kuli średnicę, nie promień. (średnicy) jest proporcjonalna do objętości części wspólnej dwóch kul o rozmiarze , których środki są odległe od siebie o (patrz rys. 4.6). Objętość odcinka kuli, czyli połowa części wspólnej dwóch kul o promieniu wynosi [4]:
 |
4.1.4 Rozkład wielkości ziaren
- Rozkład wielkości ziaren
-
(Grain Size Distribution, ) to gęstość prawdopodobieństwa znalezienia ziarna o rozmiarze (zwykle: średnicy) . W zależności od kontekstu odnosi się do liczby lub łącznej objętości ziaren o rozmiarze z przedziału . W mikroskopii, gdzie wyznacza się licząc na zdjęciu ziarna różnych rozmiarów mowa jest zawsze o w wersji “liczbowej”. W metodach rentgenowskich, gdzie mierzony efekt jest proporcjonalny do objętości materiału rozpraszającego używa się o wersji “objętościowej” (volume fraction) . W tej pracy wszędzie używamy drugiej postaci.
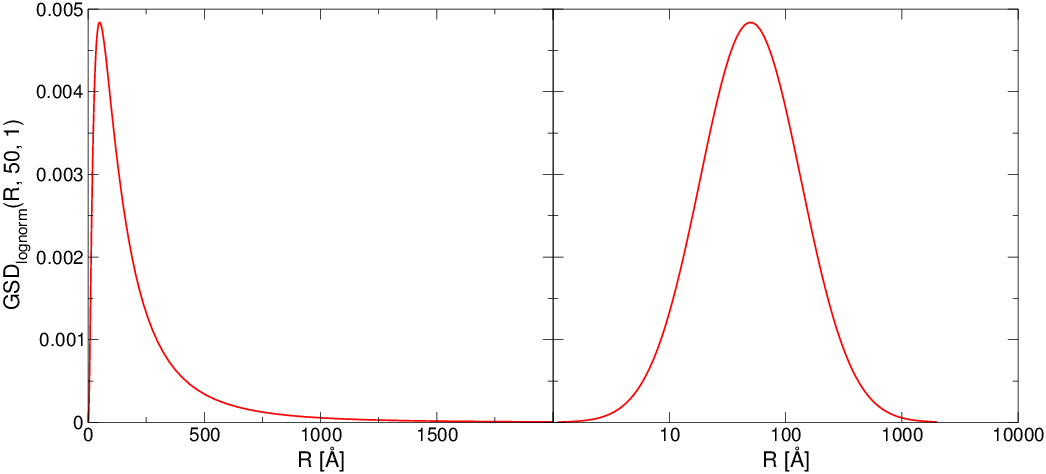
jest jedną z podstawowych wielkości charakteryzujących mikrostrukturę proszków. Zależnie od metody otrzymywania przyjmuje różną postać. Dla proszków nanometrowych jest to najczęściej rozkład log-normalny:
| (4.5) |
gdzie jest wartością średnią zaś dyspersją rozkładu normalnego zmiennej losowej (nie samego )55 5 Indeks przy symbolu dyspersji podkreśla, że odnosi się ona do rozkładu normalnego zmiennej , w odróżnieniu do dyspersji rozkładu log-normalnego zmiennej . [29], rys. 4.7. Wartość oczekiwana rozkładu log-normalnego wynosi:
| (4.6) |
moment rzędu drugiego:
| (4.7) |
zaś dyspersja66 6 Należy wyraźnie odróżnić zmienne tradycyjnie opisujące rozkład log-normalny ( i ) od wartości oczekiwanej i dyspersji tego rozkładu. Niektóre rozkłady, np. normalny, w naturalny sposób parametryzowane są wielkościami i , jednak nie jest tak w przypadku rozkładu log-normalnego (ma wtedy bardzo skomplikowaną postać).:
| (4.8) |
Wygodnym parametrem rozkładu jest tzw. współczynnik zmienności (Coefficient of Variation, CV, ), będący miarą względnej szerokości rozkładu. Oblicza się go przez podzielenie dyspersji przez wartość oczekiwaną. Dla rozkładu log-normalnego wynosi on:
| (4.9) |
Powszechnie używa się modyfikacji rozkładu log-normalnego odwołującej się nie do (mediany rozkładu normalnego zmiennej ), lecz do maksimum rozkładu log-normalnego, :
| (4.10) |
W dalszym ciągu “rozkład log-normalny” będzie oznaczał jego wersję zmodyfikowaną (4.10), chyba, że zostanie wyraźnie zasygnalizowane użycie wersji podstawowej (4.5). Wielomodowy rozkład log-normalny jest sumą rozkładów jednomodowych:
gdzie sumowanie przebiega po wszystkich modach rozkładu. Asymetryczność rozkładu log-normalnego (rys. 4.7) odzwierciedla niezerowe prawdopodobieństwo znalezienia w proszku ziaren dużo większych niż średnie (istnieje szansa na wykrystalizowanie dużych krystalitów), przy ostrym ograniczeniu wielkości ziaren od dołu.
4.1.5 Funkcja korelacji warstw
Rozważmy zespół statystyczny składający się z dużej liczby nieskończonych, kryształów o strukturze najgęstszego upakowania77 7 W szczególności mogą to być politypowe struktury nieuporządkowane. (patrz rys. 5.5). Umieśćmy każdy z nich w osobnym, kartezjańskim, prawoskrętnym układzie współrzędnych w następujący sposób:
-
1.
Niech płaszczyzny krystaliczne () kryształu będą równoległe do płaszczyzny układu.
-
2.
Jednostką osi i niech będzie stała sieci .
-
3.
Jednostką osi niech będzie odległość między sąsiednimi warstwami ( będzie wtedy numerować warstwy).
-
4.
Niech jeden z atomów warstwy będzie umieszczony w punkcie . Warstwę tą nazwijmy88 8 Umawiamy się nazywać warstwy przesunięte o ; ; . (tzn. znajdującą w pozycji ).
-
5.
Niech jego odpowiednik w warstwie będzie99 9 Skoro nazwaliśmy warstwę ’’, warstwa musi być ’’ lub ’’. Wymagamy teraz, żeby była ona właśnie ’’. Można to wymusić obracając w razie potrzeby kryształ wokół osi o ° (co przeprowadza wszystkie warstwy ’’ na ’’ i odwrotnie). umieszczony w punkcie . Warstwę tą nazwijmy (tzn. znajdującą w pozycji ).
Opiszmy sekwencję politypową pojedynczego kryształu ciągiem liter odpowiadających pozycjom warstw, np. . Warunki 4 i 5 możemy teraz zapisać następująco:
| (4.11) |
W ten sposób definiujemy pozycję i skrętność kryształu.
Funkcją korelacji warstw (Layer Correlation Function, ) , , nazywamy prawdopodobieństwo1010 10 Ściśle rzecz biorąc jest to prawdopodobieństwo warunkowe przy warunkach ustalonych w pkt.4 i 5, tzn. że w zawsze znajduje się warstwa , zaś w zawsze znajduje się warstwa . tego, że -ta warstwa kryształu będzie odpowiednio w pozycji lub :
| (4.12) |
gdzie jest numerem warstwy; indeksuje pozycje warstw ( lub ); indeks numeruje kryształy; oznacza deltę Kronecker’a, zaś opisuje sekwencję politypową -tego kryształu.
Dla poszczególnych warstw wyrażenie (4.12) przyjmuje następujące postacie:
| (4.13) |
| (4.14) |
| (4.15) |
Jak widać, w przypadku gdy funkcje korelacji warstw redukują się do postaci , , .
Funkcja korelacji warstw opisuje stopień jednowymiarowego nieuporządkowania struktury najgęstszego upakowania, rys.4.8.
a)
|
b)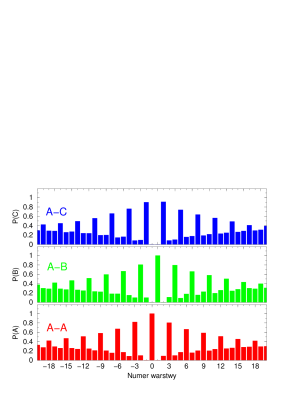
|
c)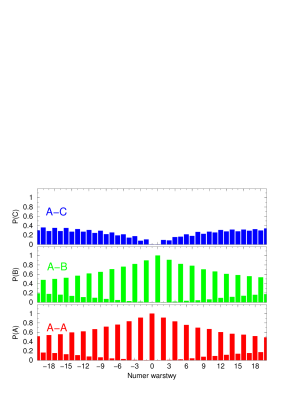
|
d)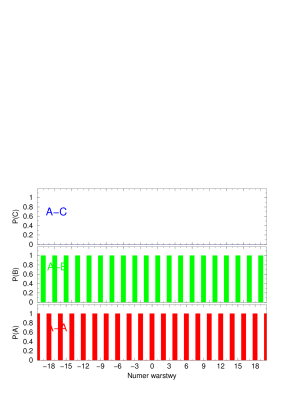
|
Dla struktur uporządkowanych (periodycznych w kierunku krystalograficznym ) jest periodyczna i ma okres równy okresowi struktury. Dla struktur nieuporządkowanych 1111 11 Na rys. 4.8 skrótowe oznaczenia oznaczają , i . jest zbieżna do stałej wartości (rys.4.8b,c). W tym przypadku zbieżność jest słaba (osiągana jest dla ). Dla struktur silnie nieuporządkowanych (gdzie parametr hexagonalności ) zbiega do bardzo szybko - już dla warstw będących najbliższymi sąsiadami warstwy odniesienia .
4.2 Numeryczne obliczanie dyfraktogramów proszkowych
Natężenie promieniowania rozproszonego przez dowolny1212 12 zarówno krystaliczny jak amorficzny układ atomów, dane w jednostkach elektronowych, wynosi [6]:
| (4.16) |
gdzie i są atomowymi czynnikami rozpraszania odpowiednich atomów oraz ; jest wektorem rozpraszania, zaś odległością pomiędzy tymi atomami. Natężenie jest uśrednione po wszystkich orientacjach przestrzennych. Wzór Debye’a użyty dla układu atomów tworzących pojedynczy krystalit, dostarcza w efekcie dyfraktogram proszku złożonego z takich właśnie, przypadkowo zorientowanych krystalitów.
Potencjalnie, metodą prób i błędów, można dopasować krzywą obliczoną przy pomocy (4.16) do doświadczalnych danych dyfrakcyjnych [23]. Niestety, czas obliczania dyfraktogramu dla jednego ziarna jest proporcjonalny do szóstej potęgi jego rozmiaru. Obliczenia bezpośrednie (tak jak formuła Debye’a stanowi) są przez to nieefektywne dla ziaren większych od ok. . Dalej zostaną przedstawione zostaną sposoby na ominięcie tego ograniczenia. Zostanie też pokazane jak można w obliczeniach dyfrakcji prowadzonych ab initio (metodą Debye’a) uwzględniać rozkład wielkości oraz uśrednione jednowymiarowe nieuporządkowanie nanokryształów.
4.2.1 Metoda bezpośrednia, funkcja korelacji par
Rozważmy substancję składającą się z rodzajów atomów, np. i w przypadku , (). Zbiór wszystkich możliwych par atomów można podzielić na podzbiorów par tego samego typu1313 13 Oczywiście, pary i , np. i są równoważne z punktu widzenia wzajemnych odległości międzyatomowych w parze, tak więc zamiast podzbiorów można by utworzyć tylko . Jednak dla prostoty zostaniemy przy ., np. , , i . Możemy indeksować wszystkie typy par jako , gdzie opisuje skład pary, np. , , i .
Teraz równanie Debye’a (4.16) można przepisać:
| (4.17) |
gdzie pierwsze dwie sumy są po wszystkich typach par, dwie ostatnie - po wszystkich parach tego samego typu. Ponieważ wielu1414 14 szczególnie w kryształach parom w wewnętrznej sumie odpowiada ta sama odległość międzyatomowa , wygodnie jest skonsolidować wszystkie odległości przez wprowadzenie histogramu odległości międzyatomowych, czyli Funkcji Korelacji Par (Pair Correlation Function, ), rys. 4.9:
| (4.18) |
gdzie jest deltą Diraca.
a)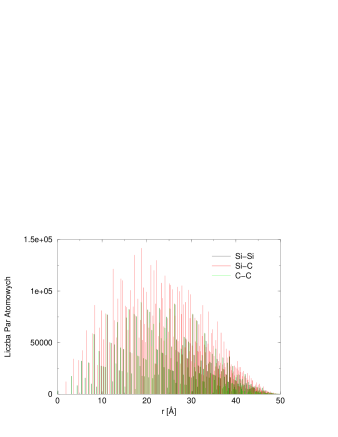
|
b) 
|
Zmodyfikowane równanie Debye’a (4.17) przyjmuje postać:
lub:
| (4.19) |
gdzie jest wielkością (średnicą) modelu. Operując funkcją korelacji par unormowaną do jedności (por. rys. 4.2a i b), należy (4.19) dodatkowo pomnożyć przecz całkowitą liczbę par atomów w krystalicie. Ponieważ:
całka w (4.19) jest transformatą furierowską, a dokładniej: transformatą sinusów funkcji . W praktyce używa się szybkiej transformaty Fouriera (Fast Fourier Transform, ), odrzucając jej część rzeczywistą (cosinusową):
| (4.20) |
Korzystając z (4.20) można obliczyć dyfraktogram proszkowy dowolnego klastera atomów bez względu na jego strukturę, uporządkowanie czy skład, zarówno w zakresie rozpraszania niskokątowego () jak i dyfrakcji bragowskiej, rys. 4.10. Część niskokątowa krzywej zawiera charakterystyczne oscylacje o okresie , gdzie jest wielkością ziarna. Biorą się one z nadreprezentacji odległości odpowiadających wielkości ziarna, przy całkowitym braku odległości większych i mniejszych. Mamy tu do czynienia ze sztucznym modelem proszku składającego się z ziaren identycznej wielkości (proszek monodyspersyjny), podczas gdy w rzeczywistości zawsze mamy do czynienia z dyspersją rozmiarów ziaren (o czym mowa w dalszej części).
a)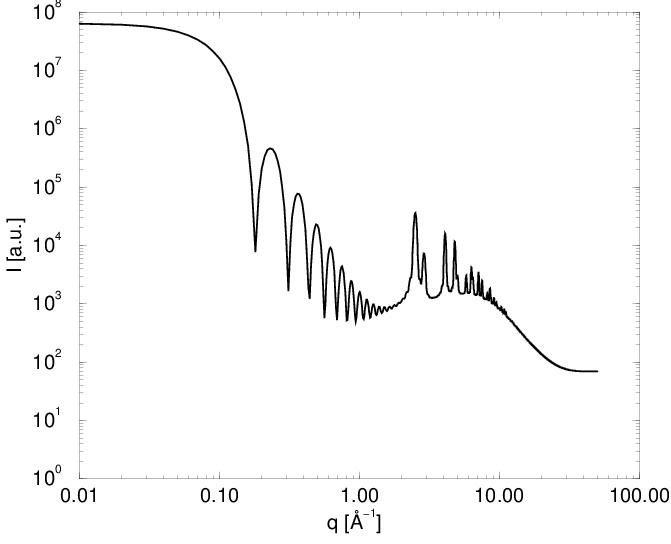
|
b)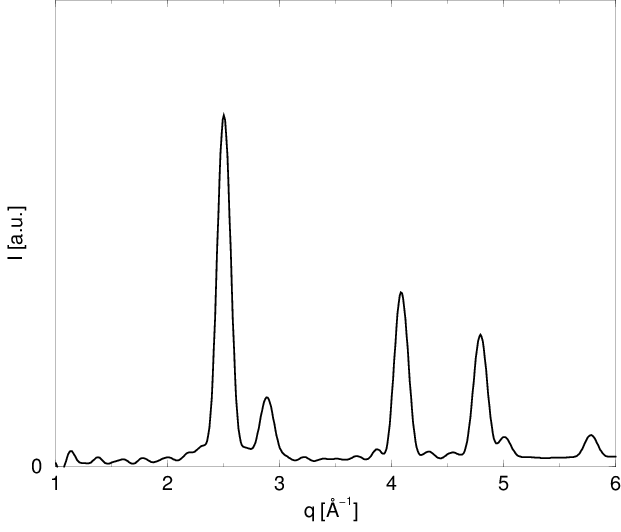
|
Bezpośrednie obliczenie dyfraktogramu proszkowego przy pomocy opisanej metody kosztuje operacji, gdyż liczba atomów w modelu , więc obliczenie wymaga kroków. można obliczyć szybciej używając pojęcia funkcji rozkładu radialnego i Dystrybucji Kształtu.
4.2.2 Model proszku monodyspersyjnego, RDF i dystrybucja kształtu
Funkcja jest zwykle identyfikowana z , ponieważ jest funkcją względnej odległości pary atomów (§4.1.2.1). W układach nieskończonych (np. dla dużych kryształów) jest to prawda, jednak w ogólności wielkości te wiąże Dystrybucja Kształtu rozważanego obiektu (np. nanokryształu), rys. 4.3:
gdzie jest dystrybucją kształtu obiektu, zaś jego rozmiarem. Po wstawieniu powyższego równania do (4.20), wzór Debye’a może być przepisany do postaci:
| (4.21) |
gdzie jest rozmiarem modelu. Ponieważ wyliczenie kosztuje tylko operacji, zaś jej transformacja w polega na prostym pomnożeniu przez dystrybucję kształtu, obliczenie dyfrakcji dla modelu wielkości kilkudziesięciu przy użyciu (4.21) trwa sekundy. Aby otrzymać model fizycznego proszku konieczne jest wprowadzenie Rozkładu Wielkości Ziaren.
4.2.3 Model proszku z rozkładem wielkości ziaren
Postać rozkładu wielkości ziaren (, §4.1.4) nanoproszku zależy od mechanizmu jego syntezy. Najczęściej przyjmuje on formę rozkładu log-normalnego (rys. 4.7) jednomodowego:
lub wielomodowego:
gdzie sumowanie przebiega po wszystkich modach rozkładu. Aby wprowadzić niezerową dyspersję rozmiarów ziaren proszku, należy zmodyfikować dystrybucję kształtu ziarna tak, aby opisywała rozmiar nie jednego, konkretnego lecz średniego ziarna proszku. Przejście od dystrybucji kształtu ziarna do uśrednionej dystrybucji kształtu ziarna można zapisać, rys. 4.11:
lecz w praktyce:
Ponieważ rozkład log-normalny jest niezerowy dla wszystkich dodatnich argumentów, konieczne jest arbitralne ustanowienie największej użytecznej wielkości ziarna. Taką granicą może być np. , gdzie jest oczekiwanym maksimum zaś jego dyspersją.
a)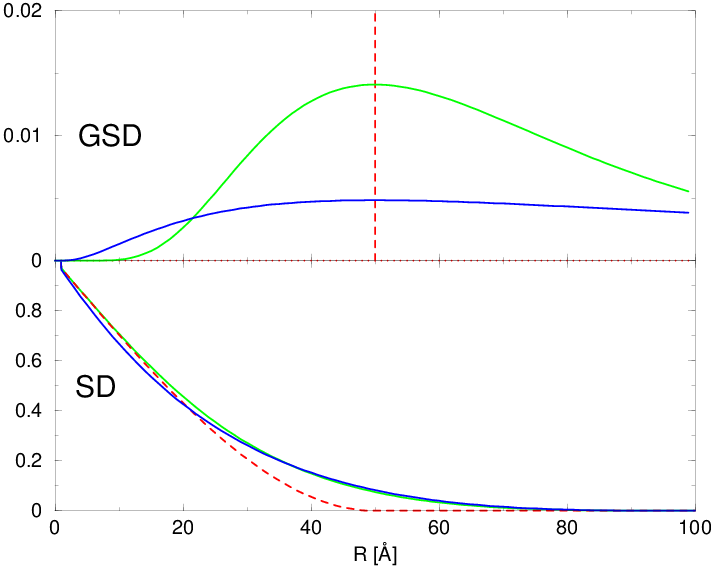
|
b)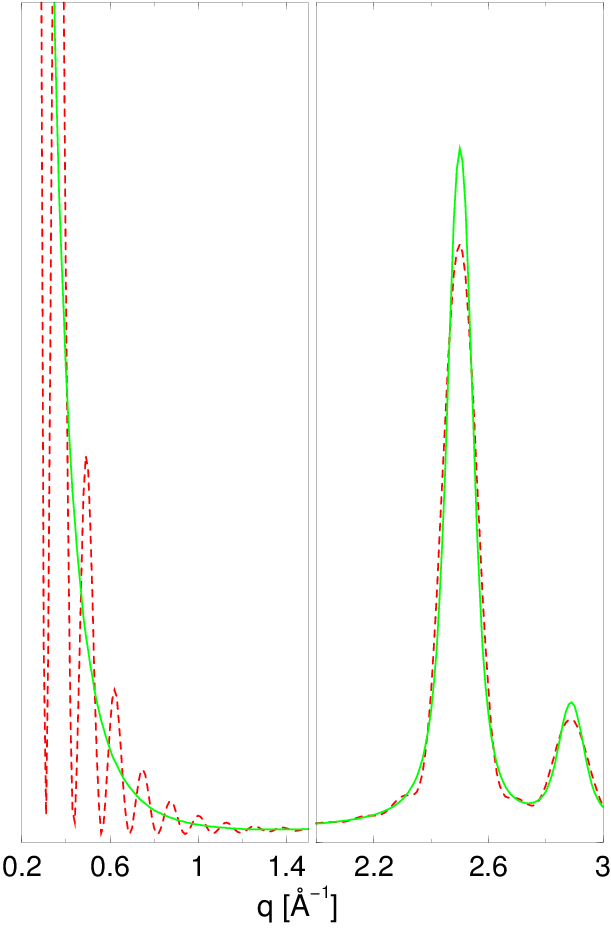
|
Dystrybucje kształtu (np. rys. 4.5 i 4.11a) są wolnozmienne i całkowalne numerycznie w zaniedbywalnym czasie. Wprowadzenie rozkładu wielkości ziaren praktycznie nie zwiększa czasu obliczeń opisanego w paragrafie 4.2.2. Zastosowanie go w obliczeniach dyfrakcji przeprowadza natomiast proszek monodyspersyjny w polidyspersyjny, który dobrze opisuje rzeczywistość fizyczną. Widać to chociażby poprzez porównanie profili dyfrakcyjnych, rys. 4.11b. Dyfraktogramy obliczone metodą Debye’a z uwzględnieniem rozkładu wielkości ziaren stanowią dobre przybliżenie krzywych mierzonych eksperymentalnie.
a)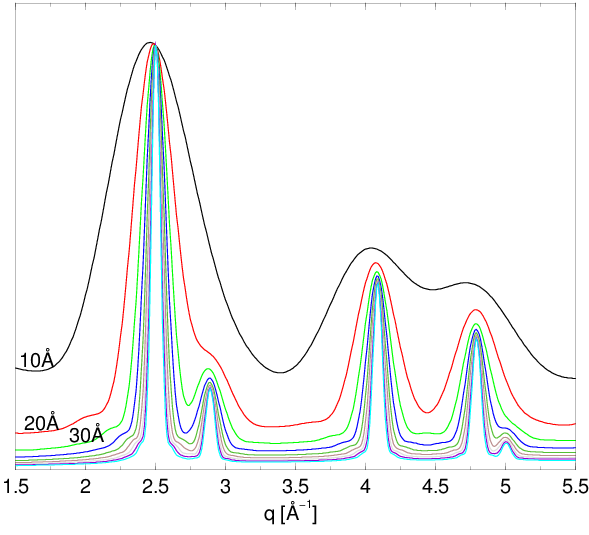
|
b)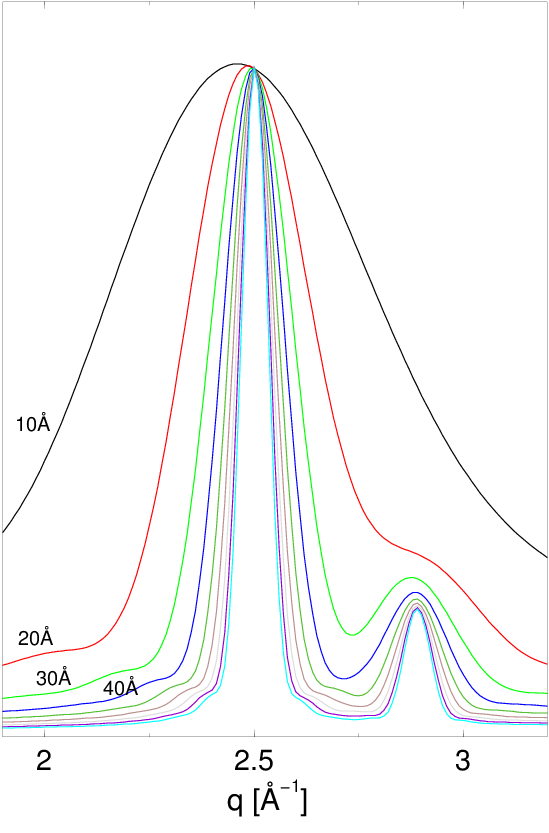
|
4.2.4 Model proszku polidyspersyjnego dla kryształów z błędami ułożenia
W nanokryształach o strukturze najgęstszego upakowania (np. , , ) możliwa jest obecność błędów ułożenia. Ich obecność łamie symetrię hexagonalną kryształu, co silnie wpływa na zjawisko dyfrakcji.
Błędy ułożenia mają naturę statystyczną i dlatego mogą być opisane przez prawdopodobieństwo ich wystąpienia, czyli (parametr hexagonalności, patrz §5.1.2.2).
Aby obliczyć profil dyfrakcyjny nieuporządkowanego nanokryształu, konieczna jest znajomość funkcji rozkładu radialnego, odpowiadającej jego strukturze. Ponieważ błędy ułożenia są rozmieszczone losowo w całej długości kryształu, otoczenie żadnego z atomów nie może być traktowane jako średnie w skali całego kryształu. Rozwiązaniem mogłoby być wielokrotne obliczenie otoczenia jednego atomu dla zmieniających się konfiguracji błędów ułożenia (losowanych z prawdopodobieństwem ), po czym wzięcie średniej. Jest to jednak metoda kosztowna obliczeniowo. W niniejszym paragrafie zaproponujemy efektywną metodę obliczania funkcji uśrednionej po wszystkich konfiguracjach błędów ułożenia danych prawdopodobieństwem .
4.2.4.1 Wielowarstwowa RDF,
Wielokrotne obliczanie przypadkowych sekwencji politypowych może być sprowadzone do jednokrotnego obliczenia wszystkich możliwych sekwencji. Każda warstwa w strukturze najgęstszego upakowania występuje w jednej z trzech możliwych pozycji: lub . Można stworzyć model struktury krystalicznej zawierający obsadzone atomami wszystkie pozycje ( i ) w każdej warstwie. Tworzy się tym samym 3-krotnie gęstsza sieć krystaliczna, Tab.4.1.
| Warstwa | Fizyczna struktura 3C | Model struktury M-L |
|---|---|---|
| 1 | ..C..C..C..C..C..C | ABCABCABCABCABCABC |
| 2 | .B..B..B..B..B..B. | ABCABCABCABCABCABC |
| 3 | A..A..A..A..A..A.. | ABCABCABCABCABCABC |
| 4 | ..C..C..C..C..C..C | ABCABCABCABCABCABC |
| 5 | .B..B..B..B..B..B. | ABCABCABCABCABCABC |
| 6 | A..A..A..A..A..A.. | ABCABCABCABCABCABC |
| 7 | ..C..C..C..C..C..C | ABCABCABCABCABCABC |
| 8 | .B..B..B..B..B..B. | ABCABCABCABCABCABC |
| 9 | A..A..A..A..A..A.. | ABCABCABCABCABCABC |
Każdy atom takiej zagęszczonej (niefizycznej) sieci może być atomem odniesienia, gdyż jego otoczenie odpowiada średniemu w całym krysztale. takiej struktury zawiera wszystkie możliwe odległości międzyatomowe które mogą się pojawić przy jakichkolwiek potencjalnych sekwencjach politypowych.
 |
 |
Aby przeprowadzić taką wielowarstwową funkcję rozkładu radialnego (Multi-Layer Radial Distribution Function, ) w odpowiadającą pewnemu konkretnemu modelowi nieuporządkowania, muszą być zastosowane określone reguły wyboru dla odległości międzyatomowych (niektóre odległości w niefizycznej są bardziej prawdopodobne, niektóre niemożliwe). Te reguły wyboru wyrażone są przez funkcję korelacji warstw (Layer Correlation Function, ), rys. 4.8, i razem z prowadzą do uśrednionego po sekwencjach politypowych występujących we wszystkich ziarnach proszku:
| (4.22) |
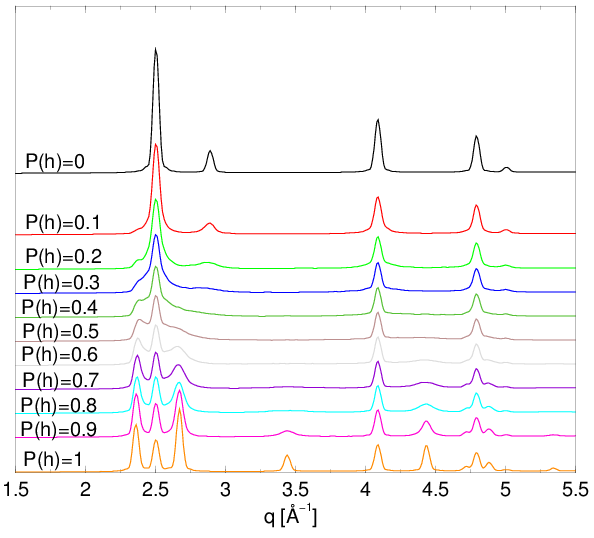
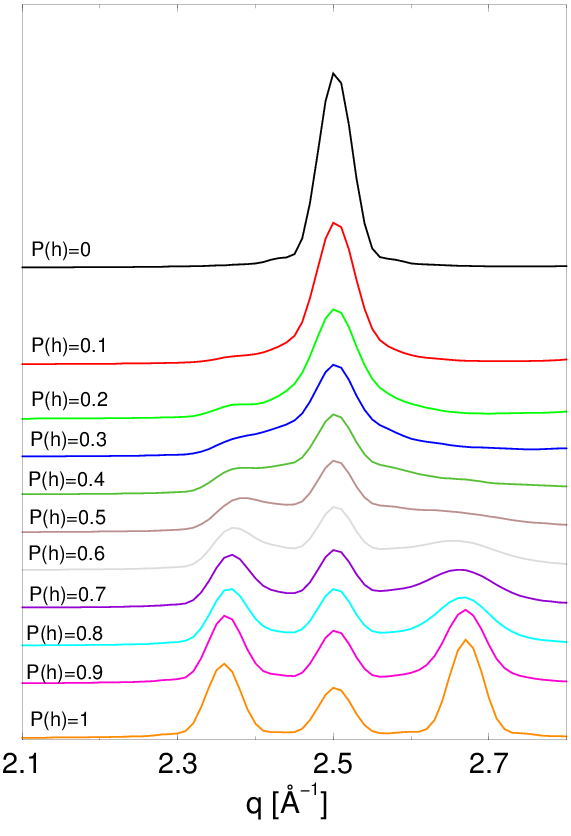
gdzie jest liczbą warstw w strukturze, jest pozycją warstwy ( lub ). Dla struktur nieuporządkowanych jest zbieżna do stałej wartości (rys. 4.8b,c). Dla struktur silnie nieuporządkowanych () funkcja nabiera sensu fizycznego już przy drugich sąsiadów:
| (4.23) |
Aby obliczyć dyfraktogram dla modelu proszku posiadającego jednocześnie:
-
•
log-normalny rozkład wielkości ziaren, rys. 4.12
-
•
dowolną konfigurację błędów ułożenia zadaną przez , rys. 4.13.
i znając niosącą informację o średnim otoczeniu atomowym w całym proszku (uśrednionym po lokalnym nieporządku wszystkich konkretnych ziaren), można użyć wzoru (4.21) zastępując przez .