Chapter 2 Ustalanie rozmiaru krystalitów
2.1 Zasada działania
W metodach obrazowych, np. w mikroskopii, obserwujemy obraz materiału zbliżony do rzeczywistego. W metodach spektroskopowych\nomenclatureSpektroskopiametoda badania materiałów polegająca na obserwacji spektrum (widma) energii emitowanego lub absorbowanego przez materiał, który oświetlono odpowiednio dobranym promieniowaniem wzbudzenia. Np. po oświetleniu marchewki światłem białym (pełne widmo widzialne) wyemituje ona tylko część tego widma odpowiadającą kolorowi pomarańczowemu, ponieważ pozostała część widma zostanie zaabsorbowana przez wiązania chemiczne karotenu obecnego w marchwii.\nomenclatureWidmo, spektrumzależność (krzywa) natężenia promieniowania w funkcji energii (albo długości fali będącej odwrotnością energii). Np. widmo emisyjne palącej się zapałki to bardzo szeroka, ciągła krzywa dzwonowa z maksimum w okolicy podczerwnieni aż do koloru żółtego. Widmo emisyjne lasera He-Ne to bardzo wąski pik dla długości fali 632.8nm (kolor czerwony) i zero natężenia gdziekolwiej indziej., interferencyjnych i dyfrakcyjnych obserwujemy piki\nomenclaturePik, liniabardzo ostre (wysokie a wąskie) lokalne maksimum, czyli ostre maksima, wskazujące na jakąś szczególną własność materiału. W przypadku dyfrakcji rentgenowskiej wyraźne piki są dowodem występowania w materiale pewnych odległości międzyatomowych nieporównanie częściej od innych.
Funkcja rozkładu radialnego. Statystykę odległości międzyatomowych pomaga zanalizować funkcja opisująca prawdopodobieństwo znalezienia atomu w odległości od wybranego atomu odniesienia (początku układu współrzędnych) nazywana funkcją rozkładu radialnego, czyli Radial Distribution Function . Na rys. 2.1 pokazano struktury i odpowiadające im funkcje dla gazów, szkieł, kryształów i nanokryształów.

W gazie cząsteczki doświadczają dość odległych, swobodnych przelotów. Oddziaływania pomiędzy cząsteczkami sprowadzają się do zderzeń, nie ma siły utrzymującej cząsteczki we w miarę stałej odległości od siebie. Dlatego dystanse między cząsteczkami są przypadkowe, zaś prawdopodobieństwo znalezienia atomu w odległości rośnie w sposób ciągły jak (kwadratowo, ponieważ tak rośnie powierzchnia sfery o promieniu , na której szukamy atomów). Dla gazu jest więc parabolą.
W przypadku szkła i innych ciał amorficznych mamy sytuację podobną do cieczy przechodzonej: cząsteczki są w bezpośrednim sąsiedztwie, ale ich ruch względem siebie jest “zamrożony”, jak stopklatka filmu. Odległości między najbliższymi sąsiadami są dość zbliżone (ale nie identyczne), dlatego ma wyraźne maksimum dla odpowiadającego odległości do pierwszych sąsiadów. Maksima odpowiadające odległości do drugich, trzecich i kolejnych sąsiadów są coraz bardziej rozmyte, ponieważ niedookreślenie odległości najbliższych sąsiadów kumuluje się wraz z sięganiem do kolejnych. Owo niedookreślenie odległości powiększone w przypadku sięgania do drugich, trzecich i dalszych sąsiadów odpowiednio 2, 3 i więcej razy w końcu robi się większe niż same odległości międzycząsteczkowe (błąd ponad 100%) i prawdopodobieństwo znalezienia odległego atomu rośnie dalej monotonicznie, bez maksimów, jak w gazie. Nazywamy to brakiem dalekiego uporządkowania.
W przypadku kryształu idealnego (nieskończonego, bez błędów strukturalnych czy naprężeń) odległości do pierwszego i kolejnych sąsiadów są ściśle określone. W krysztale idealnym funkcja prawdopodobieństwa znalezienia atomu będzie miała ostre piki w odległościach kolejnych sąsiadów, wszędzie indziej wyniesie zero, ponieważ z definicji nie znajdziemy w krysztale idealnym atomu w pozycji międzywęzłowej.
Przypadek nanokryształu jest podobny do kryształu idealnego - krystalit11 1 Terminów krystalit, nanokryształ i ziarno będziemy używać zamiennie. We wszystkich przypadkach chodzi o ograniczony przestrzennie kryształ. W przypadku nanokryształów mówimy zazwyczaj o rozmiarach nie większych niż . jest wycięty z nieskończonego kryształu idealnego, więc sieć krystaliczna krystalitu dziedziczy symetrię kryształu ale jest ograniczona przestrzennie.
Dystrybucja kształtu, Funkcja korelacji par. Matematyczną realizacją wycinania krystalitu z nieskończonej struktury krystalicznej jest pomnożenie wartości funkcji kryształu idealnego przez wartość funkcji opisującej zewnętrzny obrys krystalitu, zwanej dystrybucją kształtu, Shape Distribution . Uzyskany histogram odległości międzyatomowych nazywamy funkcją korelacji par, Pair Correlation Function , ponieważ podaje on liczbę par atomów w krystalicie odległych od siebie o :
| (2.1) |
Oczywiście, największa odległość międzyatomowa w krystalicie to dystans między atomami leżącymi na przeciwległych jego końcach, np. na biegunach krystalitu w kształcie kuli. Funkcja znika (jest zawsze zero) dla odległości większych niż ten dystans. Dystrybucja kształtu jest tylko obwiednią nałożoną na , dlatego piki i są w identycznych miejscach (patrz rys. 2.1), różnią się tylko natężeniami (czyli wysokością).
Dystrybucja kształtu krystalitu zaczyna się od wartości , tzn. , ponieważ prawdopodobieństwo znalezienia w krystalicie atomu odległego o zero (czyli jego samego) jest . Potem dystrybucja kształtu krystalitu monotonicznie maleje (pierwszych sąsiadów nie mają atomy powierzchniowe, drugich sąsiadów - kolejne wgłąb krystalitu, itd.) i osiąga zero tuż za największą odległością obecną w krystalicie (dla żadnego atomu odniesienia z krystalitu nie można znaleźć atomu w tym samym krystalicie w odległości większej niż największy wymiar krystalitu). Tak więc miejsce zerowania się dystrybucji kształtu krystalitu wyznacza jego największy rozmiar.
 |
 |
Dystrybucja kształtu ma prostą interpretację geometryczną (rys. 2.2), którą po raz pierwszy (wedle mojej wiedzy) pokazali Stokes i Wilson w latach czterdziestych [51]. Prawdopodobieństwo znalezienia odległości międzyatomowej w krystalicie, w pewnym kierunku jest proporcjonalne do objętości części wspólnej tego krystalitu i jego własnej kopii (“cienia”) przesuniętego względem oryginału o odległość w kierunku . Oczywiście, kopie krystalitu rozsunięte bardziej niż o wielkość krystalitu nie będą miały części wspólnej. Po podzieleniu objętości części wspólnej przez objętość krystalitu dostajemy unormowaną dystrybucję kształtu , tzn. dla prawdopodobieństwo będzie 1.
Zasadą działania rentgenowskich metod pomiaru wielkości krystalitów jest fakt, że bezpośrednio obserwowalny profil piku rentgenowskiego jest transformatą Fourier’a dystrybucji kształtu krystalitu opisującej jego obrys:
| (2.2) |
gdzie jest profilem linii dyfrakcyjnej (funkcją dzwonową opisującą kształt piku jak na rys. 2.4), a to Fourier Transform, czyli transformata Fourier’a.
Rysunek 2.3 pokazuje dyfraktogramy nanoproszku wyliczone dla krystalitów o różnych rozmiarach. Szerokość linii silnie zależy od rozmiaru ziarna. Znając zatem profil linii dyfrakcyjnej (piku rentgenowskiego) możemy wyznaczyć dystrybucję kształtu krystalitu, czyli informację o uśrednionym obrysie wszystkich krystalitów oświetlonych wiązką promieni rentgenowskich22 2 Zwykle oświetlamy ok. próbki na głębokość kilku, np. mikronów. Daje to ok. rozpraszającego materiału, czyli jednocześnie analizujemy ponad nanokryształów (zakładając rozmiar i nawet bardzo luźno nasypany proszek). Zatem informacja niesiona przez rozproszone promienie X jest statystycznie dość kompletna..
a)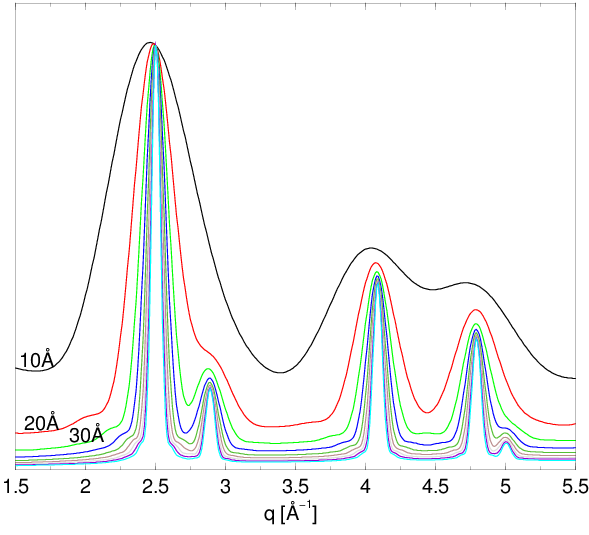
|
b)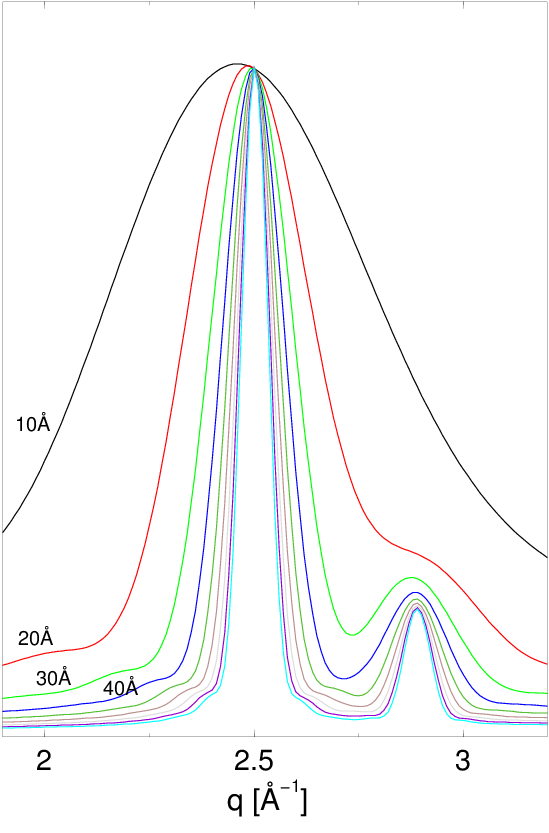
|
c)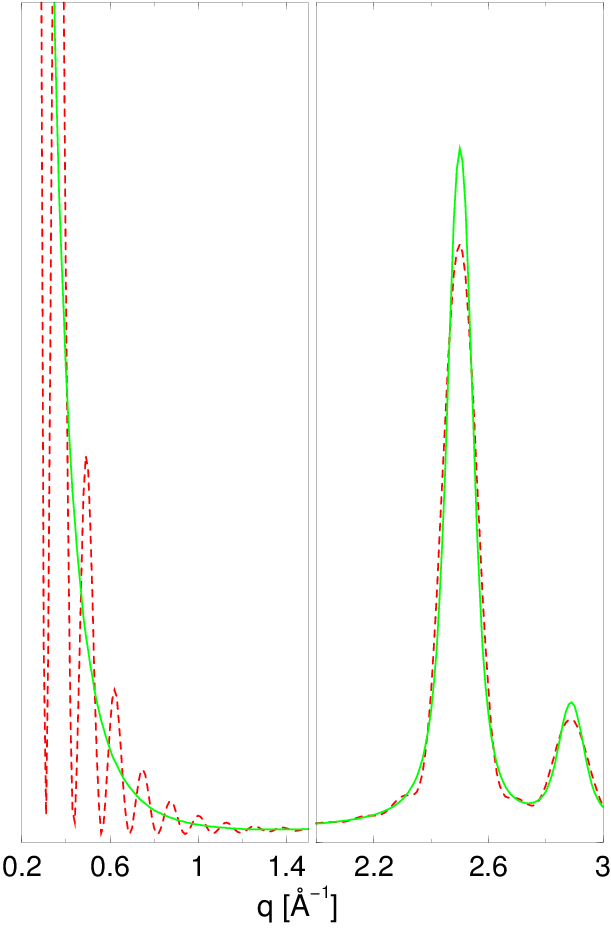
|
Informacja o mikrostrukturze nanoproszku obecna w danych XRD jest bardzo bogata, co sprawia, że istnieje wiele metod jej analizy i prezentacji. Dalej zaprezentujemy kilka wybranych, możliwie prostych w użyciu i pożytecznych. Dla dociekliwych, w rozdziale zatytułowanym Podstawy fizyczne pokażemy skąd biorą się najważniejsze zależności. Niecierpliwi mogą ten rozdział bezpiecznie pominąć.
2.2 Proszki monodyspersyjne
2.2.1 Metoda Scherrer’a
a) b)
b)
Metoda Scherrer’a jest najczęściej używaną techniką szybkiego szacowania rozmiaru krystalitów. Wykorzystuje ona fakt, że szerokość połówkowa linii dyfrakcyjnej jest dla proszków monodyspersyjnych (wszystkie ziarna identycznego rozmiaru) odwrotnie proporcjonalna do rozmiaru krystalitu (3.32). Równanie Scherrer’a w jednostkach wektora rozpraszania jest:
| (2.3) |
gdzie jest stałą Scherrer’a, zaś to Full Width at Half Maximum, czyli szerokość piku w połowie jego wysokości, nazywana też szerokością połówkową. Równanie Scherrer’a (2.3) podaje rozmiar krystalitów w Ångström’ach, czyli dla uzyskania nanometrów wynik należy podzielić przez . Szerokość połówkowa jest dana w jednostkach wektora rozpraszania [Å], czyli w Ångström’ach odwrotnych. Pamiętając o zależności (3.86) można zapisać równanie Scherrer’a dla skali kąta jako:
| (2.4) |
gdzie jest szerokością połówkową wyrażoną w stopniach skali . We wzorze (2.4) długość fali i rozmiar mają te same jednostki, tzn. jeśli podajemy w [Å] to otrzymamy rozmiar w [Å], jeśli podajemy w [] otrzymamy rozmiar w []. Należy zwrócić uwagę, że pod cosinusem jest , a nie , więc kąt pod którym zmierzono maksimum należy przed wstawieniem do cosinusa podzielić przez dwa. Stała Scherrer’a jest bezwymiarowa, wbrew nazwie nie jest stała (zależy głównie od kształtu krystalitu) i wynosi około jedności. Dalej wyliczymy ją dla dwóch ważnych przypadków: kryształów prostopadłościennych () i o kształcie zbliżonym do kuli ().
Najważniejszą zaletą metody Scherrer’a jest prostota. Wadą jest jej zachowanie dla proszków polidyspersyjnych (mieszanina krystalitów o różnych rozmiarach): wbrew rozpowszechnionemu poglądowi, obliczany z niej rozmiar nie jest w takich przypadkach ani rozmiarem średnim, ani medianą, ani inną dobrze zdefiniowaną statystyczną miarą rozmiaru (dlatego mówi się czasem o “rozmiarze Scherrer’a”), rys. 2.4a. Niestety, większość realnie występujących proszków jest polidyspersyjna, dlatego dalej podamy sposoby ominięcia tego kłopotu.
Granice stosowalności metody Scherrer’a w jej oryginalnej postaci zostały określone w §3.5.8.
Przykład. Dla piku dyfrakcyjnego z rys. 2.4b mamy:
2.3 Proszki polidyspersyjne
Polidyspersyjność proszku oznacza, że jego ziarna nie są tego samego rozmiaru, tylko mamy mieszaninę ziaren o różnych rozmiarach (pewien rozrzut wielkości). Ten rozrzut opisywany jest rozkładem wielkości ziaren, Grain Size Distribution , rys. 2.5.
Rozkład wielkości ziaren jest to krzywa określająca prawdopodobieństwo wystąpienia (w proszku) ziarna o rozmiarze . Do zdefiniowania rozkładu używa się zwykle (aczkolwiek niekoniecznie) dwóch parametrów: średniego rozmiaru i dyspersji , będącej miarą rozrzutu rozmiarów wokół wartości średniej . Im dyspersja mniejsza, tym ziarna mniej się od siebie różnią i szerokość krzywej jest mniejsza. Oba parametry mają wymiar długości, zwykle []. Dyspersja jest miarą szerokości rozkładu wielkości ziaren i jej podwojona wartość, czyli , odpowiada mniej-więcej szerokości połówkowej tego rozkładu, rys. 2.5. Pomocna bywa też bezwymiarowa, względna szerokość rozkładu wielkości, wzięta z podzielenia jego dyspersji przez średnią: .
Funkcji matematycznych mogących służyć za przybliżenie faktycznego rozkładu wielkości ziaren materiału są dziesiątki. Wybór funkcji rozkładu zależy od przyjętego mechanizmu syntezy proszku33 3 Np. Kołmogorow wykazał [31], że wszelkie procesy związane z rozdrabnianiem (mieleniem) prowadzą do rozkładu log-normalnego, informacji eksperymentalnych44 4 Np. fotografie SEM i TEM mogą naprowadzić na postać rozkładu wielkości grającego rolę w konkretnej próbce., własności matematycznych ułatwiających jego użycie55 5 Np. całkowalność albo istnienie momentów wyższych rzędów wynikających z przyjętej teorii., a najczęściej - od wszystkich tych czynników jednocześnie. Częstym wyborem jest rozkład log-normalny.
W teorii dyfrakcji jedyny jak dotąd rozkład statystyczny prowadzący do analitycznych (czyli w miarę prostych) formuł opisujących natężenie rozproszonego promieniowania to rozkład wykładniczo-potęgowy, rys. 2.5. W granicach dostępnych precyzji pomiarowych jego krzywizna jest praktycznie identyczna z najpopularniejszym rozkładem log-normalnym, rys. 2.7. Wykładniczo-potęgowy rozkład wielkości ziaren ma postać:
| (2.5) |
gdzie jest stałą normującą, jest funkcją gamma Eulera, zaś i są pewnymi parametrami możliwymi potem do wyrażenia jako średni rozmiar ziarna i dyspersja rozmiarów .

Dla ustalenia samego średniego rozmiaru ziarna w proszku polidyspersyjnym, można użyć prostej metody Integral Breadth (§2.3.1), która pozwala wyliczyć statystycznie poprawny rozmiar średni tylko na podstawie dwóch natężeń66 6 Tu pokażemy unowocześnioną i uproszczoną wersję klasycznej metody Integral Breadth. piku: integralnego i maksymalnego.
Ustalenie rozkładu wielkości ziaren w proszkach polidyspersyjnych najprościej uzyskać przy pomocy metody Scherrer’a uzupełnionej o drugi parametr szerokości linii (metoda , patrz §2.3.2). W oryginalnej metodzie Scherrer’a, do rozwiązania równania z jedną niewiadomą (rozmiar) wystarczyła jedna dana: szerokość piku zmierzona w połowie jego wysokości. W metodzie , do ustalenia dwóch niewiadomych (rozmiar średni i dyspersja rozmiarów) potrzebne są dwie dane, np. dwie szerokości linii zmierzone odpowiednio na i wysokości piku. Dalej pokażemy jak to zrobić.
Inna możliwość to bezpośrednie dopasowanie funkcji profilu linii do pików doświadczalnych. Jest to zapewne technika optymalna, bo pozwala na uzyskanie najlepszej dokładności i wychwycenie ewentualnych osobliwości w danych (np. asymetryczne piki). Może ona jednak stwarzać niedoświadczonym lub po prostu bardzo zajętym eksperymentatorom kłopot z powodu dużej pracochłonności. Dlatego pokażemy sposób użycia usługi on-line, która pozwala uzyskać potrzebne informacje wprost z danych dyfrakcyjnych w kilkanaście sekund.
2.3.1 Metoda Integral Breadth (uogólniona)
Historycznie, metoda Integral Breadth (poszerzenia całkowitego) została opracowana przez Stokes’a i Wilson’a w latach 40-tych XX-tego wieku. Polegała ona na zastąpieniu w równaniu Scherrer’a (2.4) szerokości piku mierzonej w połowie jego wysokości przez szerokość integralną, tj. szerokość prostokąta o powierzchni i wysokości równej odpowiednio powierzchni i wysokości piku. Powierzchnia piku nazywana jest jego natężeniem całkowitym albo natężeniem integralnym i dotyczy powierzchni pod pikiem razem z jego ramionami do (teoretycznie) nieskończoności. Natężenie integralne piku można uzyskać dodając zliczenia ze wszystkich punktów pomiarowych tworzących pik77 7 Niestety, w przypadku, kiedy piki na siebie nachodzą albo tło jest znaczące i nierówne sytuacja nieco się komplikuje - trzeba wtedy użyć odpowiednich programów fitujących. Proponujemy także przeczytać uwagi na temat określania poziomu tła w sekcji 2.4.3. i mnożąc tę sumę przez krok licznika (jednostkowy kąt pomiaru). Wysokość piku odczytujemy bezpośrednio ze skali natężeń (oś rzędnych) w razie potrzeby odejmując od natężenia maksimum poziom tła (jeśli tło jest znaczące).
Korzystając z (3.91) prezentujemy uogólnioną ale jednocześnie prostszą i dokładniejszą wersję metody Integral Breadth, niewymagającą podawania kąta i stałej Scherrer’a. Dla ziaren zbliżonych do kuli (najczęstszy przypadek) średni rozmiar wynosi:
| (2.6) |
gdzie jest natężeniem zmierzonym w maksimum piku, jest natężeniem integralnym piku, jest średnim rozmiarem krystalitów danym w [Å]. Należy pamiętać, że natężenie integralne (powierzchnię piku) można otrzymać z sumy natężeń wszystkich punktów piku mnożąc ją przez krok pomiaru i przeliczając do jednostek wektora rozpraszania (3.93). Natężenie integralne piku można zatem zapisać jako:
| (2.7) |
gdzie jest sumą natężeń wszystkich zmierzonych punktów piku, zaś to długość pojedynczego kroku goniometru w skali . Na przykład, dla piku zmierzonego w zakresie od do skali z krokiem mielibyśmy punktów i , oczywiście. Kąt jest położeniem środka analizowanej linii; należy pamiętać o podzieleniu przez 2 pozycji linii wziętej z tradycyjnej skali .
W ogólnym przypadku średni rozmiar ziarna wynosi:
| (2.8) |
gdzie jest parametrem zależnym od kształtu krystalitu i kierunku krystalograficznego. Parametr wynosi (rys. 2.6):
-
•
dla kryształów prostopadłościennych w kierunkach czołowych (np. ),
-
•
dla kryształów zbliżonych kształtem do kuli (niezależnie od kierunku),
-
•
dla kryształów prostopadłościennych w kierunkach krawędziowych (np. ),
-
•
dla kryształów prostopadłościennych w kierunkach wierzchołkowych (np. ).
 |
|
| (a) | |
| (b) | |
| (c) | |
Główną zaletą metody jest podawanie rzeczywiście średniego rozmiaru ziarna, bez względu na postać i szerokość rozkładu wielkości ziaren. Kolejną zaletą jest prostota (o ile dysponujemy wiarygodnym określeniem natężenia integralnego piku, co nie jest trudne, patrz §2.4.3). Wadą jest brak informacji o szerokości rozkładu wielkości ziaren (dyspersji) i konieczność przyjęcia jakiegoś kształtu ziarna. Niestety, ta ostatnia wada jest w metodach rentgenowskich trudna do wyeliminowania88 8 Informacja o kształcie ziarna jest, co prawda, zawarta w dystrybucji kształtu krystalitu, ale jej wiarygodne wydobycie wymagałoby natężeń rzędu setek tysięcy i milionów zliczeń w maksimum piku. Takie natężenia nie są dostępne, na dzień dzisiejszy, poza najsilniejszymi synchrotronami, więc podawanie odpowiednich receptur mijałoby się z celem., §2.5. W przypadkach wątpliwych zapewne najczęstszym wyborem będzie kształt podobny do kuli.
Przykład. Dla piku dyfrakcyjnego z rys. 2.4b mamy:
2.3.2 Metoda Scherrer’a uogólniona,
Metoda Scherrer’a, wspaniale działająca dla proszków monodyspersyjnych, niestety zawodzi w przypadku mieszaniny ziaren o różnych rozmiarach, rys. 2.4. W przypadku polidyspersyjnym potrzebujemy uzyskać nie jeden parametr rozmiaru, a dwa: rozmiar średni i dyspersję . Aby uogólnić metodę Scherrer’a na przypadek polidyspersyjny potrzeba więc dostarczyć więcej informacji: zamiast pojedynczej szerokości w połowie wysokości, , należy zmierzyć na tym samym piku dwie szerokości na różnych wysokościach, np. na i jego maksimum, czyli odpowiednio: i .
Korzystając z dalej wyprowadzonych zależności (3.85) i (3.86), podajemy wzory na średni rozmiar ziarna i dyspersję w proszku polidyspersyjnym jako funkcję bezpośrednio mierzalnych szerokości i proszkowej linii dyfrakcyjnej:
| (2.9) | |||||
gdzie pomocnicze współczynniki i wynoszą99
9
Proszę zwrócić uwagę, że istnieją przynajmniej dwie popularne definicje
arccot (cotangensa odwrotnego): ciągła i symetryczna. Tutaj korzystamy
z wersji symetrycznej:  .:
.:
zaś pozostałe parametry to: - długość fali padającego promieniowania rentgenowskiego oraz - połowa kąta , pod którym zmierzono analizowaną linię dyfrakcyjną. Szerokości i dane są w skali .
Otrzymane wartości i mają jednostki takie same jak podana długość fali , tzn. jeśli podano w [], to oba parametry rozkładu też będą dane w [], jeśli jest wyrażona w [Å], to i także będą mianowane w [Å].
Na rys. 2.7 przedstawiono przykłady oznaczeń rozkładu wielkości ziaren metodą dla dyfraktogramów proszkowych\nomenclatureDyfraktogram proszkowyzależność (krzywa) natężenia promieniowania rentgenowskiego ugiętego przez proszek (zwykle krystaliczny) od kąta wiązki pierwotnej. Założeniem dyfrakcji proszkowej jest, że każdy krystalit w proszku jest zorientowany przypadkowo i krystalitów jest nieskończenie wiele. Dzięki temu, jeśli licznik fotonów znajduje się pod kątem odbicia (bragowskim) mierzonego materiału, to zawsze znajdzie się jakiś krystalit zorientowany właściwie względem wiązki pierwotnej i licznika tak, żeby skierować rozproszone fotony z wiązki do licznika. wyliczonych teoretycznie (ab initio1010 10 Określenie “ab initio” jest używane także w chemii kwantowej na opis jednej z metod obliczeniowych. Zbieżność nazw jest przypadkowa - obliczenia numeryczne dyfrakcji nie mają związku z chemią kwantową.). Przedstawione dyfraktogramy zostały wyliczone przy założeniu log-normalnego rozkładu wielkości ziaren. Na tak otrzymanym dyfraktogramie dokonano pomiaru szerokości linii oraz na i wysokości, użyto wzorów (3.85) otrzymując parametry i . Następnie wykreślono na ich podstawie rozkład wielkości ziaren (3.51), widoczny w dolnej części rys. 2.7 (czerwona krzywa) razem z log-normalnym rozkładem wielkości ziaren użytym podczas obliczania profili dyfrakcyjnych (czarna, urwana krzywa). Z rys. 2.7 widać, że użyty wykładniczo-potęgowy rozkład wielkości ziaren dobrze emuluje rozkład log-normalny w praktycznych zastosowaniach.
 |
 |
 |
 |
 |
 |
Bezpośredni pomiar szerokości piku może być technicznie kłopotliwy. Istnieje proste rozszerzenie metody polegające na dopasowaniu piku popularną funkcją Pearson VII i prostym przeliczeniu wartości otrzymanych z fitowania na szerokości oraz . Opisano to w §2.3.5.1 i §3.5.5.1.
Przykład. Dla piku dyfrakcyjnego z rys. 2.4b mamy:
2.3.3 Metoda Warren’a-Averbach’a
W 1950 roku Warren i Averbach przedstawili metodę wyznaczania średniego rozmiaru krystalitów oraz rozkładu ich wielkości na podstawie kształtu maksimów dyfrakcyjnych [54]. Wybrane maksimum dyfrakcyjne typu , po niezbędnych korektach (odjęcie tła, korekty na poszerzenie instrumentalne, itp.) rozwija się w szereg cosinusów w zakresie obejmującym oba jego ramiona do miejsc, gdzie natężenie znika, rys. 3.18. Początek układu współrzędnych oraz wierzchołek maksimum umieszcza się w środku tego zakresu (rys. 3.18b). Współczynniki rozwinięcia dane są przez:
| (2.10) |
gdzie jest ciągiem punktów pomiarowych tworzących badany refleks w funkcji wektora rozpraszania ( jest natężeniem w maksimum linii, rys. 3.18b); jest całkowitą szerokością analizowanego refleksu; określa odległość w przestrzeni prostej odpowiadającą współczynnikowi . Otrzymane z rozwinięcia (2.10) wartości współczynników układają się na szybko malejącej krzywej (rys. 3.18c). Druga pochodna krzywej tworzonej przez współczynniki rozwinięcia jest rozkładem długości kolumn komórek elementarnych (, Column Length Distribution), z wagą proporcjonalną do objętości każdej kolumny:
| (2.11) |
Rozkład wyraża więc ułamek objętości kryształu przypadający na kolumny o różnych długościach (rys. 3.19b). Krzywa (2.11) bywa interpretowana jako rozkład wielkości krystalitów. Jak pokazano w §3.5.9, poza szczególnymi przypadkami, uzyskanie rozkładu wielkości krystalitów tą techniką jest trudne lub niemożliwe. Można natomiast uzyskać średni rozmiar ziarna, pod warunkiem, że (i) znamy lub założymy przybliżony kształt ziarna oraz (ii) proszek jest monodyspersyjny. Rozmiar ziarna dostaje się przez pomnożenie średniej długości kolumn komórek elementarnych przez stałą właściwą dla kształtu ziarna (np. dla ziaren kulistych). Wielkość dostaje się z przecięcia osi z extrapolowaną prostą poprowadzoną przez pierwsze punkty ciągu . Choć stopień pracochłonności analizy danych tą metodą jest większy niż np. dla metody Scherrer’a czy Integral Breadth, jej ograniczenia (i wyniki) są podobne.
W tabeli 2.1 zestawiamy wielkości otrzymywane z analizy W-A dla proszków o różnych mikrostrukturach, czyli wartości oraz wartości błędów metody dla najczęściej spotykanych przypadków.
| Rodzaj proszku | |||||
| formuła | |||||
| pojedyncze kuliste ziarno | - | - | |||
| wykładniczo-potęgowy | |||||
| log-normalny | |||||
| dowolny | - | - | - | ||
Zależność średniej długości kolumn od szerokości rozkładu wielkości ziaren oznacza, że w realnych przypadkach do uzyskania rozmiaru ziaren metodą Warren’a-Averbach’a potrzebna jest znajomość dyspersji ich rozkładu wielkości. Ogranicza to stosowalność metody do proszków (prawie) monodyspersyjnych lub dobrze znanych (np. pochodzących z jednego źródła). W przypadku proszków polidyspersyjnych obraz mikrostruktury może być zniekształcony (możliwe błędy rzędu nawet 100% i więcej). Metoda Warren’a-Averbach’a nie umożliwia wyznaczenia pełnego rozkładu wielkości ziaren (poza szczególnymi przypadkami)1111 11 Sami autorzy nie przypisywali jej zresztą takiej własności. Mowa o tym dopiero w pracach pochodnych. Obiegową opinię ukształtowały jednak te ostatnie, nie oryginał. ani nie podaje dyspersji rozmiarów .
2.3.4 Nanokryształy dużych molekuł
Skrajnie małe rozmiary kryształów nanometrowych są szczególnie kłopotliwe w interpretacji danych rentgenowskich dla materiałów złożonych ze stosunkowo dużych molekuł (lub komórek elementarnych). Założeniem dyfrakcji rentgenowskiej jest, że komórka elementarna kryształu, w której mieści się jedna (czasem więcej) molekuł związku chemicznego budującego kryształ, jest powielona w krysztale bardzo, bardzo, bardzo wiele razy. Podobnie jak wielki dom zbudowany z małych cegieł. Nazywamy to symetrią translacyjną, w ramach której obserwator przeskakując do sąsiedniej komórki elementarnej kryształu widziałby takie samo otoczenie jak z poprzedniej: a więc niekończący się szereg komórek elementarnych w każdym kierunku. W przypadku małych molekuł nieorganicznych, takich jak NaCl, to założenie jest nieźle spełnione: ich komórki elementarne mają po kilka Å są więc rzędy wielkości mniejsze od nanokryształów, nawet , a tym bardziej większych.
Niektóre materiały mają jednak duże komórki elementarne i stałe sieci rzędu i więcej. Ich kryształ o rozmiarach kilku zawierałby tylko kilka komórek elementarnych w każdym kierunku. Jest to spory kłopot, bowiem mamy tu niekorzystny splot dwóch efektów: duża komórka elementarna oznacza zwykle wiele blisko sąsiadujących pików rentgenowskich (gęsty “las”), zaś mały rozmiar kryształu oznacza, że piki te są bardzo szerokie. W efekcie bliskie sobie, szerokie piki nakładają się i zamiast izolowanych maksimów obserwujemy ciągłą, mocno pofałdowaną funkcję natężenia, rys. 2.8. Niestety, większość metod rentgenowskich polega na analizie pików rentgenowskich, a więc maksimów natężenia w przestrzeni odwrotnej. Brak izolowanych pików utrudnia lub wyklucza wykonanie takiej analizy. W przypadkach pośrednich (nakładające się piki, ale jednak rozróżnialne) możliwe jest użycie narzędzi matematycznych dopasowujących (fitujących) do danych doświadczalnych przewidywany teoretycznie dyfraktogram. Procedura ta wymaga sporej wprawy i wielkiej pokory: łatwo jest uzyskać doskonałe dopasowanie błędnego modelu, co może wprawić niedoświadczonego eksperymentatora w przekonanie, że ustalił (mikro)strukturę materiału. Granica “analizowalności” splecionych (nakładających się) pików jest płynna; dużą sztuką jest trafne określenie tej granicy.
a) b)
b)
2.3.4.1 Analiza poza przestrzenią odwrotną
Piki nanokryształów dużych molekuł nakładają się w przestrzeni odwrotnej, często uniemożliwiając klasyczną analizę profilu linii, rys. 2.8. Na szczęście znając analityczny wzór na profil linii proszku polidyspersyjnego (3.76, 3.5.3, 3.5.3, 3.5.3) możemy stransformować ten profil do przestrzeni innych niż odwrotna1212 12 Niekoniecznie musi to oznaczać przestrzeń prostą (przestrzeń odległości międzyatomowych), ponieważ różne typy transformat (sinusowa, cosinusowa, zespolona, mocy) zastosowane kolejno w różnych porządkach dadzą informacje o różnych fizycznych interpretacjach. Ten wątek nie będzie rozwijany, wykracza poza ramy książki.. Można tam przeprowadzić operację matematyczną polegającą na scaleniu wszystkich pików obecnych na dyfraktogramie, po czym przeprowadzić analizę profilu tego (już pojedynczego) “superpiku”. Owo scalenie można porównać do hybrydyzacji znanej z chemii kwantowej. Jest to operacja stricte matematyczna, tworząca byt co prawda niefizyczny ale wygodny pojęciowo i obliczeniowo.
Procedura “piku zhybrydyzowanego” ma jasne zalety: znika problem splecionych (nakładających się) pików, rośnie natężenie analizowanej linii, a więc i dokładność analizy. Procedura ta ma też wady: wynik będzie poprawny o ile we wszystkich pikach spodziewamy się podobnego profilu, a więc sprawdzi się raczej dla materiałów jednofazowych1313 13 Trwają prace nad rozszerzeniem tej techniki na materiały wielofazowe.. Procedura jest trudna do samodzielnego zastosowania, dlatego została zaimplementowana w narzędziu internetowym http://science24.com/xrd, rys. 2.16.
Dla zanalizowania dyfraktogramu z silnie splecionymi pikami należy przeciągnąć plik z danymi XRD do dużego żółtego pola na stronie i tam go upuścić, rys. 2.15. Dane zostaną przesłane na serwer obliczeniowy, a wynik obliczeń mikrostruktury w postaci rozkładu wielkości ziaren po kilku sekundach zostanie wyświetlony w okienku aplikacji1414 14 Obecnie obsługiwane są wyłącznie materiały jednofazowe. W przypadku wykrycia dwóch faz lub znaczącego dodatku fazy amorficznej, narzędzie powinno zatrzymać analizę i poinformować o niespełnieniu założeń jej protokołu., rys. 2.16.
2.3.5 Metody bezpośredniego dopasowania
a) b)
b)
Wyrażenie (3.76) opisuje kształt piku dyfrakcyjnego. Technicznie, jest to krzywa dzwonowa (rys. 2.4) podoba do krzywej Gaussa i może być bezpośrednio dopasowana do danych doświadczalnych. Typowo, dyfraktogram składa się z wielu pików dyfrakcyjnych, rys. 2.9a. Przy pomocy (3.76) można dopasować wszystkie piki lub tylko niektóre z nich. Do dopasowywania (ang. fitting) danych doświadczalnych stosuje się specjalistyczne programy komputerowe. Większość (jeśli nie wszystkie) posiadają możliwość zdefiniowania funkcji użytkownika. Wprowadzając tam (jednorazowo) nieco długi wzór (3.76) uzyskujemy bezpośrednio informacje o rozkładzie wielkości krystalitów, ponieważ parametrami fitowania są wielkości oraz mające bezpośrednią fizyczną interpretację i po zakończeniu fitowania (zwykle kilka sekund) otrzymujemy ich wartości. Dla ułatwienia, wzór (3.76) oraz jego pochodną wydrukowano (rys. 2.10) jako kod QR (zobacz także rozdział Chapter 6 Dodatki). Można go wczytać przy pomocy telefonu komórkowego, gdzie pojawi się jako zwykły tekst, zawierający wzór matematyczny zapisany w składni języka C/C++. Stamtąd łatwo przenieść go (np. wysyłając sobie e-mail’em) do komputera i skopiować do programu fitującego jako funkcję użytkownika. Można też wkleić go do własnego kodu obliczeniowego.
 |
 |
| , wzór (3.76) | - pochodna |
| (pow(Rsr,3)*(3*pow(1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2), pow(Rsr,2)/(2.*pow(sigma,2)))* (2 + (pow(q,2)*(-3 + pow(Rsr,2)/pow(sigma,2))* (-2 + pow(Rsr,2)/pow(sigma,2))*pow(sigma,4))/pow(Rsr,2)\ ) - 6*pow(1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2),1.5)* cos((-3 + pow(Rsr,2)/pow(sigma,2))* atan((q*pow(sigma,2))/Rsr)) - (6*q*(-3 + pow(Rsr,2)/pow(sigma,2))*pow(sigma,2)* (1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2))* sin((-2 + pow(Rsr,2)/pow(sigma,2))* atan((q*pow(sigma,2))/Rsr)))/Rsr))/ (sqrt(2*M_PI)*pow(q,4)*(-3 + pow(Rsr,2)/pow(sigma,2))* (-2 + pow(Rsr,2)/pow(sigma,2))*(-1 + pow(Rsr,2)/pow(sigma,2))* pow(sigma,6)*pow(1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2), pow(Rsr,2)/(2.*pow(sigma,2)))) | (3*sqrt(2/M_PI)*(-(Rsr*pow(1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2), pow(Rsr,2)/(2.*pow(sigma,2)))* (pow(q,2)*pow(Rsr,4) + 6*pow(q,2)*pow(sigma,4) + pow(Rsr,2)*(4 - 5*pow(q,2)*pow(sigma,2)))) - pow(q,2)*Rsr*(pow(Rsr,4) - 5*pow(Rsr,2)*pow(sigma,2) + 6*pow(sigma,4))*cos((-2 + pow(Rsr,2)/pow(sigma,2))* atan((q*pow(sigma,2))/Rsr)) + Rsr*sqrt(1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2))* ((pow(q,2)*pow(sigma,4) + pow(Rsr,2)*(4 + pow(q,2)*pow(sigma,2)))* cos((-3 + pow(Rsr,2)/pow(sigma,2))* atan((q*pow(sigma,2))/Rsr)) + q*Rsr*(pow(Rsr,2) - 3*pow(sigma,2))* sin((-3 + pow(Rsr,2)/pow(sigma,2))* atan((q*pow(sigma,2))/Rsr))) + q*(pow(Rsr,2) - 3*pow(sigma,2))* (pow(q,2)*pow(sigma,4) + pow(Rsr,2)*(3 + pow(q,2)*pow(sigma,2)))* sin((-2 + pow(Rsr,2)/pow(sigma,2))* atan((q*pow(sigma,2))/Rsr))))/ (pow(q,5)*pow(1 + (pow(q,2)*pow(sigma,4))/pow(Rsr,2), pow(Rsr,2)/(2.*pow(sigma,2)))* (pow(Rsr,6) - 6*pow(Rsr,4)*pow(sigma,2) + 11*pow(Rsr,2)*pow(sigma,4) - 6*pow(sigma,6))) |
Istnieje także szereg specjalistycznych programów komputerowych służących do analizy danych dyfrakcyjnych, w tym do dopasowywania całych dyfraktogramów. Wiele z nich jest dostępnych pod adresem http://www.ccp14.ac.uk/mirror/mirror.htm.
Na rys. 2.9 pokazano przykład dopasowania krzywych dzwonowych profili pików polidyspersyjnych (ziarna kuliste) danych wzorem (3.76) do danych doświadczalnych. Dopasowano jednocześnie trzy nakładające się piki, a następnie porównano otrzymane rozkłady wielkości ziaren z analogicznymi rozkładami pochodzącymi z analizy zdjęć mikroskopii TEM1515 15 Podziękowania dla A.Opalińskiej, C.Leonelli, H.Matysiaka..
2.3.5.1 Dopasowanie Pearson VII dla metody
Programy fitujące zwykle mają kilka predefiniowanych profili używanych do dopasowań. Często obecna jest krzywa nazywana Pearson VII. Jest to praktycznie funkcja Lorentz’a podniesiona do potęgi (), która jest jednym z parametrów Pearson VII. Użycie Pearson VII do dopasowania danych doświadczalnych pozwala szybko obliczyć rozkład wielkości ziaren nanoproszku korzystając “po drodze” z metody , rys. 2.11.

Rozwiązując proste równanie (patrz §3.5.5.1) można opisać szerokości piku na i jego maksimum za pomocą parametrów i funkcji Pearson VII:
| (2.12) | |||||
| (2.13) |
W ten sposób, dostając w wyniku fitowania funkcji Pearson VII wartości parametrów oraz , dostajemy automatycznie wielkości oraz . Możemy je zatem wstawić bezpośrednio do wzorów (2.9), jeżeli dane doświadczalne były w funkcji . W przypadku danych w funkcji wektora rozpraszania , wielkości oraz należy wstawić do prostszych wzorów (3.85).
2.3.6 Narzędzia internetowe
2.3.6.1 Science24.com/tth2q
Proste narzędzie dostępne pod adresem http://science24.com/tth2q/ pozwala na konwersję pliku z danymi dyfrakcyjnymi w jednostkach do skali wektora rozpraszania . Formularz ma tylko dwa pola:

-
•
pole długości fali (domyślnie )
-
•
pole do wskazania pliku do przesłania (plik musi mieć format tekstowy, dwukolumnowy: + natężenie, separowane spacją lub tabulatorem)
Po przesłaniu pliku z danymi , po chwili powinno pojawić się okienko pozwalające zapisać na lokalnym dysku skonwertowany plik w skali wektora rozpraszania, rys .2.12.
2.3.6.2 Science24.com/fw145m
Bezpłatne narzędzie dostępne pod adresem http://science24.com/fw145m/ jest zestawem formularzy obliczeniowych dla wielu prezentowanych tu wielkości. Formularz ma następujące sekcje:
- Grain Size Distribution Calculator
-
wylicza i rozkładu wielkości ziaren na podstawie szerokości linii mierzonej na i jej wysokości. Szerokości muszą być podane w jednostkach wektora rozpraszania , rys. 2.13

Figure 2.13: Bezpłatne narzędzie http://science24.com/fw145m/. Formularz obliczenia rozkładu wielkości ziaren metodą . Wprowadzane wartości muszą być w jednostkach wektora rozpraszania. Przykład obliczenia rozkładu wielkości ziaren dla piku z rys. 2.4b. - Pearson VII Grain Size Distribution Calculator
- Grain Size Distribution Plotter
-
zwraca plik tekstowy zawierający krzywą wykładniczo-potęgowego rozkładu wielkości ziaren wyliczoną zgodnie z (2.5) dla zadanych w formularzu i . Format pliku to pary rozmiar-gęstość prawdopodobieństwa. Taki plik można łatwo wczytać do dowolnego programu robiącego wykresy (np. Excel), rys. 2.14.

Figure 2.14: Bezpłatne narzędzie http://science24.com/fw145m/. Formularz zapisania krzywej wykładniczo-potęgowego rozkładu wielkości ziaren jako pliku tekstowego do użycia w wykresach i prezentacjach. Przykład obliczenia rozkładu wielkości ziaren dla piku z rys. 2.4b. - <R> error estimation
- Lattice constant error estimation
2.3.6.3 Science24.com/xrd
Inną możliwością bezpośredniej analizy danych jest użycie bezpłatnej aplikacji webowej dostępnej pod adresem http://science24.com/xrd (rys. 2.15 i 2.16). Jest to zdalny pulpit serwera usług naukowych, gdzie plik z danymi dyfrakcyjnymi1616 16 Obecnie akceptowane są formaty tekstowe, tj. pliki XY, gdzie w pierwszej kolumnie każdej linii znajduje się kąt , zaś w drugiej natężenie. Obie wartości muszą być oddzielone spacją lub tabulatorem. Separatorem dziesiętnym w liczbach musi być kropka, nie przecinek. można bezpośrednio przeciągnąć do żółtego “lądowiska” ograniczonego przerywaną linią i tam go upuścić. Upuszczone dane są wysyłane na serwer, gdzie odbywa się ich analiza według teorii opisanej w tej książce. Przetwarzanie trwa typowo kilka-kilkanaście sekund, po czym do okna przeglądarki wysyłane są wyniki: oryginalny dyfraktogram w skali wektora rozpraszania, funkcja interferencyjna, krzywe rozkładu wielkości ziaren w nanometrach oraz tabela z liczbami opisującymi mikrostrukturę nanoproszku, gdzie znajdziemy m.in. parametry i . Można wysłać cały zestaw plików (zaznaczamy kilka plików i przeciągamy zaznaczenie). Można też upuścić dodatkowy plik na już obecne dyfraktogramy - zostanie wtedy dołączony do zestawu1717 17 Aplikacja jest rozwijana, dlatego lista aktualnie dostępnych funkcji może się zmieniać, niektóre mogą czasowo nie być aktywne. Filmy instruktażowe dotyczące korzystania z aplikacji dostępne są pod adresem http://science24.com/fw145m. Twórcy aplikacji będą wdzięczni za wszelkie uwagi Użytkowników. Prosimy kierować je pod adres support@science24.com. .


Na rysunku widać wynik analizy trzech dyfraktogramów hydroxyapatytu (HAP) o rozmiarach kryształów , i . Aplikacja wylicza poprawne rozkłady wielkości ziaren pomimo silnie splecionych (nakładających się) pików, ponieważ nie korzysta podczas obliczeń z przestrzeni odwrotnej. Klasyczna analiza profilu linii w przestrzeni odwrotnej byłaby bardzo trudna lub niemożliwa dla tak silnie nakładających się linii.
2.4 Oszacowanie i redukcja błędów pomiarowych
Za błędy pomiarowe w dyfrakcji rentgenowskiej rutynowo przyjmuje się liczby zwracane przez oprogramowanie fitujące dane doświadczalne. Niestety, wartości błędów uzyskiwane podczas fitowania z reguły są parametrami numerycznymi metody najmniejszych kwadratów i nie mają związku z wyznaczanymi wielkościami (np. stałą sieci) ani w ogóle z teorią dyfrakcji. Błędy tak uzyskane mogą być zaniżone, co z kolei może prowadzić do błędnych wniosków na temat badanych zjawisk fizycznych. Z tego względu poniżej prezentujemy proste oszacowanie błędów oparte na teorii dyfrakcji i raczej konserwatywne, tzn. błędy rzeczywiste nie powinny przekraczać prezentowanych, rys. 2.17.
a) b)
b)
Założeniem podanych niżej twierdzeń jest dobre dopasowanie. To znaczy, że wszystkie punkty dopasowanego profilu muszą mieścić się w zakresie szumu krzywej doświadczalnej (bardzo blisko chwilowej wartości średniej profilu doświadczalnego), w całym zakresie analizowanego piku. Złe dopasowanie danych wprowadza dodatkowy błąd systematyczny, zaś poniższe twierdzenia dotyczą tylko niepewności powodowanej szumem.
2.4.1 Błąd oznaczenia stałej sieci nanokryształów
Zgodnie z (3.137), procentowy błąd oznaczenia stałej sieci \nomenclatureStała sieci(albo parametr sieci) najmniejsza odległość, po pokonaniu której obserwator widziałby identyczny układ atomów jak przed ruchem (patrz "Symetria translacyjna"). W przestrzeni 3D są 3 stałe sieci (mogą mieć takie same albo różne wartości), zwykle oznaczane a, b i c, ponieważ możliwy jest niezależny ruch w 3 kierunkach.\nomenclatureSymetria translacyjnawłasność przestrzeni, dzięki której po przesunięciu (translacji) środka układu współrzędnych przestrzeń przechodzi sama w siebie. Np. w krysztale idealnym przeniesienie obserwatora z węzła (atomu) jednej komórki elementarnej do odpowiadającego mu węzła sąsiedniej komórki sprawi, że będzie on widział dookoła identyczny układ atomów. wynikający z ograniczonej statystyki pomiaru (liczby zliczeń) analizowanej linii można oszacować jako:
| (2.14) | |||||
| (2.15) | |||||
| (2.16) |
gdzie jest natężeniem analizowanego piku w jego maksimum (nie chodzi o natężenie integralne), danym w zliczeniach, jest przybliżonym rozmiarem krystalitów proszku w [Ångström’ach] zaś jest połową kąta bragowskiego , pod którym widoczna jest analizowana linia.

Wzór (2.14) jest wariantem ogólnym, który zapisano także dla dwóch przypadków szczególnych: (2.15) dla często używanej fali oraz (2.16) dla tejże fali i ustalonego kąta . Ten ostatni wariant został wykreślony na rys. 2.17a w funkcji rozmiaru ziarna dla czterech wariantów natężenia maximum: 10, 100, 1000, 10000 oraz 100000 zliczeń.
Błąd stałej sieci jest tym większy im krystality mniejsze, ponieważ pliki są wtedy szersze, a więc jednoznaczne ustalenie położenia piku jest odpowiednio trudniejsze. Błąd stałej sieci powiększa słaba statystyka (mało zliczeń), co oczywiste.
Pod adresem http://science24.com/fw145m/ dostępne jest bezpłatne narzędzie internetowe, które wylicza błąd stałej sieci nanokryształów spowodowany szumem, rys. 2.18.
2.4.2 Błąd oznaczenia rozmiaru ziarna nanokryształów
Zgodnie z (3.138), procentowy błąd oznaczenia rozmiaru ziarna z profilu piku dyfrakcyjnego można przybliżyć jako:
| (2.17) |
gdzie jest liczbą zliczeń w maksimum analizowanego piku. Czyli im większa liczba zliczeń (lepsza statystyka) tym mniejszy błąd oznaczenia jego rozmiaru. Wykres wielkości błędu w funkcji natężenia w maximum linii pokazano na rys. 2.17b. Narzędzie internetowe http://science24.com/fw145m/ posiada gotowy formularz obliczający ten błąd, rys. 2.19.
Przykład. Dla piku dyfrakcyjnego z rys. 2.4b mamy:

2.4.3 Określanie poziomu tła piku, reguła -3%
Większość metod rentgenowskich wymaga albo ustalenia szerokości pików na określonych wysokościach (np. w połowie maksimum) albo ustalenia integralnego natężenia piku. W obu przypadkach potrzebna jest znajomość zarówno natężenia maksimum piku (co jest łatwe) jak i efektywnego zera czyli poziomu natężenia, do którego asymptotycznie zmierzają oba ramiona piku. Ten poziom natężenia, często nazywany poziomem tła\nomenclatureTłonieużyteczne natężenie rejestrowane jednocześnie z użytecznym sygnałem, często ma postać szumu. Np. dla pików dyfrakcyjnych tłem jest natężenie od fazy amorficznej, szum aparaturowy, rozpraszanie nieelastyczne Debye’a-Waller’a, efekt Comptona, itp., to wartość, którą należy odjąć od natężeń wszystkich punktów piku aby otrzymać profil niezakłócony wpływem pików sąsiednich, szumem termicznym, szumem aparatury, efektem Comptona czy innymi komponentami natężenia związanymi ze zliczaniem kwantów “niestrukturalnych”.
Ustalenie poziomu tła wydaje się łatwym zadaniem i często wykonuje się je “na oko”, czyli odejmuje się arbitralną, ciągłą, wolnozmienną krzywą (najczęściej wielomian), zaczepiając ją w tych częściach dyfraktogramu, gdzie natężenie jest wyraźnie najmniejsze. W przypadku piku z rys. 2.4b, byłby to poziom ok. 160 zliczeń, ponieważ właśnie to natężenie (w okolicy ) stanowi lokalne minimum.
Jednakże teoria dyfrakcji, np. rys. 2.4a wskazuje, że dla nanoproszków natężenie linii spada dość wolno i w okolicy trzy- lub czterokrotności szerokości linii ciągle wynosi ok. natężenia maksimum linii.
Wynika z tego, że do oszacowania poziomu tła należy wziąć natężenie punktu odległego od centrum piku o 3-4-krotność szerokości połówkowej (na rys. 2.4b w okolicy , czyli zliczeń) i odjąć od tej wartości ok. natężenia maksimum piku (). Tak otrzymana wartość ( zliczeń) będzie bardziej poprawną estymatą poziomu tła niż wartość określona intuicyjnie.
| rozmiar średni | dyspersja | |||||
| Przyjęty poziom tła | zliczeń | zliczeń | błąd | zliczeń | zliczeń | błąd |
| Metoda Scherrer’a | - | - | - | |||
| Metoda Integral Breadth | - | - | - | |||
| Metoda | ||||||
Znaczenie określenia poziomu tła dla jakości oznaczeń rentgenowskich jest zaskakująco duże. Dla przykładu z rys. 2.4b: przy ustaleniu poziomu tła metodą intuicyjną (na zliczeń) rozmiar ziarna może być przeszacowany nawet o , tylko z uwagi na zaniżony poziom tła. Szczególnie wrażliwa na sposób odcięcia tła jest metoda Integral Breadth, ponieważ nawet niewielkie tło scałkowane po pełnej szerokości piku daje znaczący wkład w natężenie integralne, będące podstawą działania metody. Mniej wrażliwe są metody oparte na pomiarze szerokości linii. W razie istotnych i trudnych do określenia kształtów tła najlepszą techniką jest bezpośrednie dopasowanie profili linii dyfrakcyjnych opisane w sekcji 2.3.5.
2.5 Kształt krystalitów
Każda linia dyfrakcyjna jest etykietowana tzw. indexem Millera, czyli trójką liczb naturalnych , odpowiadającą rodzinie odbijających płaszczyzn krystalicznych dla tego kierunku. Tak więc piki rentgenowskie są “kierunkowe”.
Jednocześnie wiadomo, że istnieją kryształy o silnej anizotropii kształtu, np. rosnące w kształcie cienkich płytek lub długich igieł. Można powiedzieć, że ich rozmiar też jest “kierunkowy”, tzn. w jedną stronę znacząco inny niż w drugą. Np. igła o podstawie pojedynczych może mieć wysokość setek i więcej.
Skoro znamy profile pików rentgenowskich dla różnych kierunków z osobna, to również możemy wyliczyć rozmiary krystalitów dla różnych kierunków z osobna. Intuicja podpowiada, że rozmiary te powinny odpowiadać wydłużeniu kryształu w kierunku opisanym przez index Millera analizowanego piku. A więc powinniśmy być w stanie podać dość kompletny (chociaż uśredniony) kształt krystalitów.
Niestety, praktyka zdaje się nie potwierdzać intuicji, rys. 2.20. Zależność między anizotropią kryształu i kształtem pików rzeczywiście istnieje, jednak nie widać prostej odpowiedniości między kierunkiem wydłużenia kryształu i poszerzeniem odpowiedniej rodziny pików. Zależność kształt kryształu - profile linii jest bardziej złożona, dlatego ograniczymy się do stwierdzenia, że opisane wyżej metody nadają się dobrze do raczej dla kryształów objętościowych. W przypadku kryształów o dużej anizotropii kształtu należy zachować większą ostrożność.

2.6 Ograniczenia metod rentgenowskich
Informacje na temat mikrostruktury kryształów otrzymuje się z analizy profilu, czyli kształtu, pików dyfrakcyjnych. Wyżej opisane procedury pozwalają na ustalenie rozmiarów krystalitów właśnie przez analizę profilu linii. Na profil linii wpływa jednak nie tylko rozmiar kryształów. Piki mogą zostać zdeformowane np. przez obecne w krysztale naprężenia, błędy strukturalne czy artefakty powstające w czasie pomiaru (np. poszerzenie aparaturowe, rozbieżność wiązki, przesunięcie próbki, itp.). Niestety, praktycznie wszystkie wspomniane efekty powodują poszerzenie (nigdy zwężenie) linii dyfrakcyjnych, co może być błędnie uznane za dowód na mały rozmiar krystalitów (albo sztucznie pomniejszać zmierzoną wartość ich rozmiaru). Z tych względów jest rzeczą największej wagi aby pomimo dostępności automatycznych narzędzi do analizy danych, pozostawać w ścisłym kontakcie z kompetentnymi fachowcami z dziedziny dyfrakcji rentgenowskiej. Pomogą oni ustalić, czy wspomniane pasożytnicze efekty są dostatecznie małe, aby można je było zaniedbać lub wskażą skuteczne techniki analizy danych pozwalające uwzględnić te efekty.